Question and Answers Forum

All Questions      Topic List

Logarithms Questions

Previous in All Question      Next in All Question      

Previous in Logarithms      Next in Logarithms      

Question Number 196690 by MATHEMATICSAM last updated on 29/Aug/23

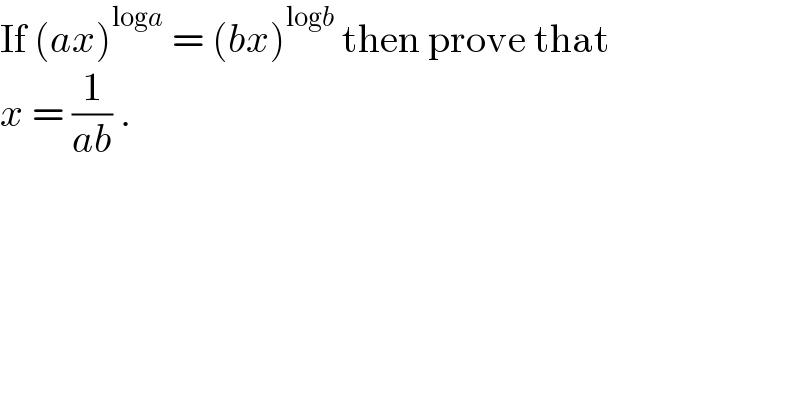
If (ax)^(loga) = (bx)^(logb) then prove that x = (1/(ab)) .

$$\mathrm{If}\:\left({ax}\right)^{\mathrm{log}{a}} \:=\:\left({bx}\right)^{\mathrm{log}{b}} \:\mathrm{then}\:\mathrm{prove}\:\mathrm{that} \\ $$$${x}\:=\:\frac{\mathrm{1}}{{ab}}\:. \\ $$

Answered by BaliramKumar last updated on 29/Aug/23

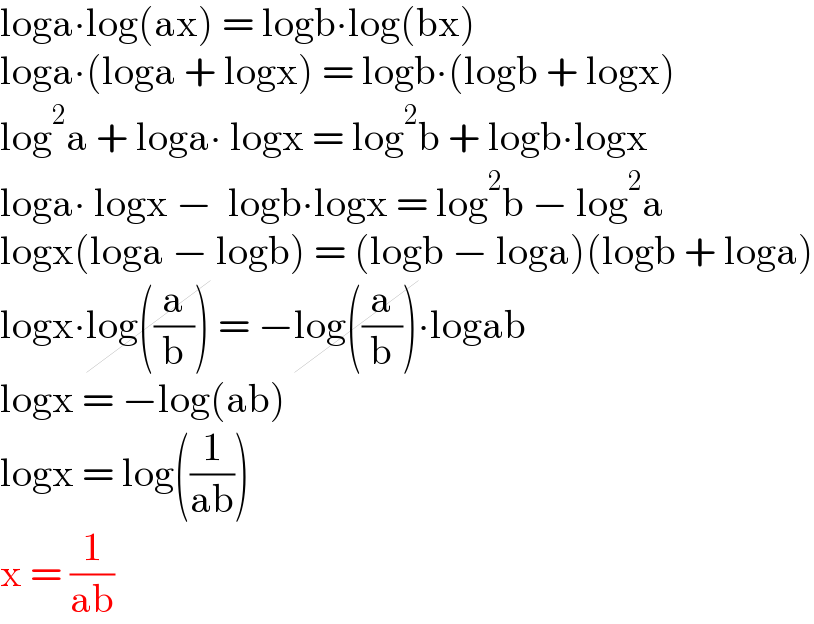
loga∙log(ax) = logb∙log(bx) loga∙(loga + logx) = logb∙(logb + logx) log^2 a + loga∙ logx = log^2 b + logb∙logx loga∙ logx − logb∙logx = log^2 b − log^2 a logx(loga − logb) = (logb − loga)(logb + loga) logx∙log((a/b)) = −log((a/b))∙logab logx = −log(ab) logx = log((1/(ab))) x = (1/(ab))

$$\mathrm{loga}\centerdot\mathrm{log}\left(\mathrm{ax}\right)\:=\:\mathrm{logb}\centerdot\mathrm{log}\left(\mathrm{bx}\right) \\ $$$$\mathrm{loga}\centerdot\left(\mathrm{loga}\:+\:\mathrm{logx}\right)\:=\:\mathrm{logb}\centerdot\left(\mathrm{logb}\:+\:\mathrm{logx}\right) \\ $$$$\mathrm{log}^{\mathrm{2}} \mathrm{a}\:+\:\mathrm{loga}\centerdot\:\mathrm{logx}\:=\:\mathrm{log}^{\mathrm{2}} \mathrm{b}\:+\:\mathrm{logb}\centerdot\mathrm{logx} \\ $$$$\mathrm{loga}\centerdot\:\mathrm{logx}\:−\:\:\mathrm{logb}\centerdot\mathrm{logx}\:=\:\mathrm{log}^{\mathrm{2}} \mathrm{b}\:−\:\mathrm{log}^{\mathrm{2}} \mathrm{a} \\ $$$$\mathrm{logx}\left(\mathrm{loga}\:−\:\mathrm{logb}\right)\:=\:\left(\mathrm{logb}\:−\:\mathrm{loga}\right)\left(\mathrm{logb}\:+\:\mathrm{loga}\right) \\ $$$$\mathrm{logx}\centerdot\cancel{\mathrm{log}\left(\frac{\mathrm{a}}{\mathrm{b}}\right)}\:=\:−\cancel{\mathrm{log}\left(\frac{\mathrm{a}}{\mathrm{b}}\right)}\centerdot\mathrm{logab} \\ $$$$\mathrm{logx}\:=\:−\mathrm{log}\left(\mathrm{ab}\right) \\ $$$$\mathrm{logx}\:=\:\mathrm{log}\left(\frac{\mathrm{1}}{\mathrm{ab}}\right) \\ $$$$\mathrm{x}\:=\:\frac{\mathrm{1}}{\mathrm{ab}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com