
Question Number 196635 by sonukgindia last updated on 28/Aug/23
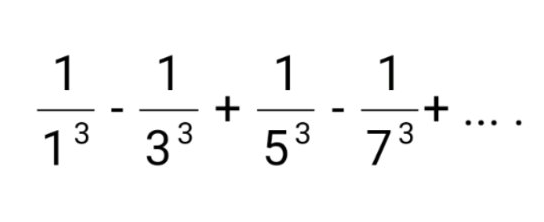
Answered by sniper237 last updated on 28/Aug/23
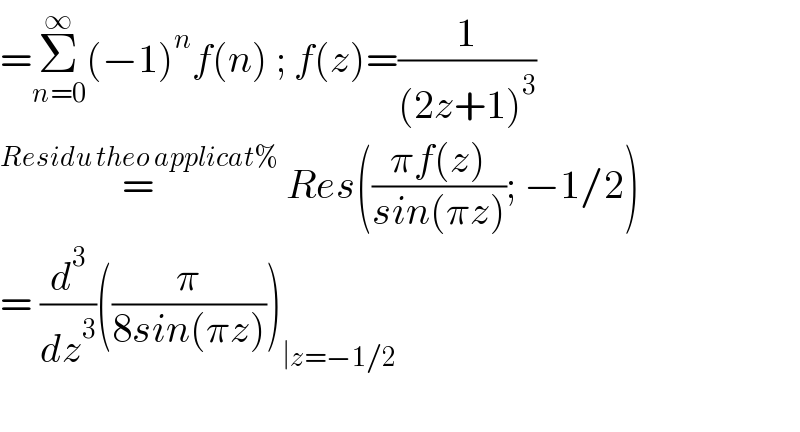
$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} {f}\left({n}\right)\:;\:{f}\left({z}\right)=\frac{\mathrm{1}}{\left(\mathrm{2}{z}+\mathrm{1}\right)^{\mathrm{3}} } \\ $$$$\overset{{Residu}\:{theo}\:{applicat\%}} {=}\:{Res}\left(\frac{\pi{f}\left({z}\right)}{{sin}\left(\pi{z}\right)};\:−\mathrm{1}/\mathrm{2}\right)\:\:\: \\ $$$$=\:\frac{{d}^{\mathrm{3}} }{{dz}^{\mathrm{3}} }\left(\frac{\pi}{\mathrm{8}{sin}\left(\pi{z}\right)}\right)_{\mid{z}=−\mathrm{1}/\mathrm{2}} \\ $$$$ \\ $$
