
Question Number 196567 by pete last updated on 27/Aug/23
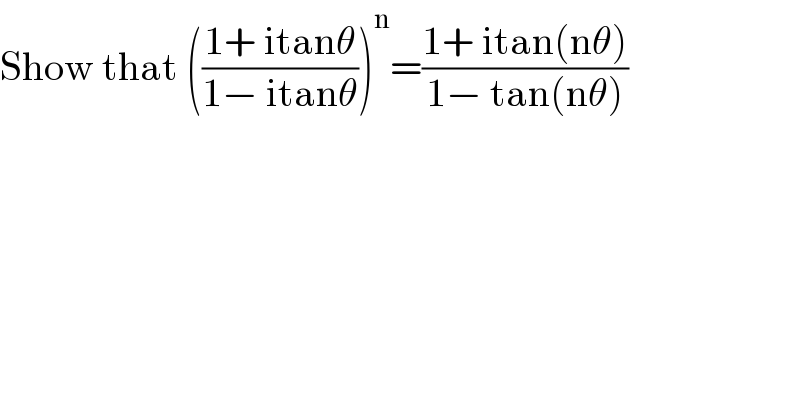
$$\mathrm{Show}\:\mathrm{that}\:\left(\frac{\mathrm{1}+\:\mathrm{itan}\theta}{\mathrm{1}−\:\mathrm{itan}\theta}\right)^{\mathrm{n}} =\frac{\mathrm{1}+\:\mathrm{itan}\left(\mathrm{n}\theta\right)}{\mathrm{1}−\:\mathrm{tan}\left(\mathrm{n}\theta\right)} \\ $$
Commented by mokys last updated on 27/Aug/23
![(((1+itanθ)/(1−itanθ)))^n =((((cosθ+isinθ)/(cosθ))/((cosθ−isinθ)/(cosθ))))^n =(((cos(nθ)+isin(nθ))/(cos(nθ)−isin(nθ)))) = ((cos(nθ) [ 1+ i ((sin(nθ))/(cos(nθ)))])/(cos(nθ)[1−i((sin(nθ))/(cos(nθ))])) = ((1+itan(nθ))/(1−itan(nθ)))](Q196569.png)
$$\left(\frac{\mathrm{1}+{itan}\theta}{\mathrm{1}−{itan}\theta}\right)^{{n}} =\left(\frac{\frac{{cos}\theta+{isin}\theta}{{cos}\theta}}{\frac{{cos}\theta−{isin}\theta}{{cos}\theta}}\right)^{{n}} =\left(\frac{{cos}\left({n}\theta\right)+{isin}\left({n}\theta\right)}{{cos}\left({n}\theta\right)−{isin}\left({n}\theta\right)}\right) \\ $$$$ \\ $$$$=\:\frac{{cos}\left({n}\theta\right)\:\left[\:\mathrm{1}+\:{i}\:\frac{{sin}\left({n}\theta\right)}{{cos}\left({n}\theta\right)}\right]}{{cos}\left({n}\theta\right)\left[\mathrm{1}−{i}\frac{{sin}\left({n}\theta\right)}{{cos}\left({n}\theta\right.}\right]}\:=\:\frac{\mathrm{1}+{itan}\left({n}\theta\right)}{\mathrm{1}−{itan}\left({n}\theta\right)} \\ $$
Commented by pete last updated on 27/Aug/23

$$\mathrm{Than}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by mokys last updated on 27/Aug/23

$${you}\:{are}\:{welcome} \\ $$
