
Question Number 196540 by Matica last updated on 27/Aug/23
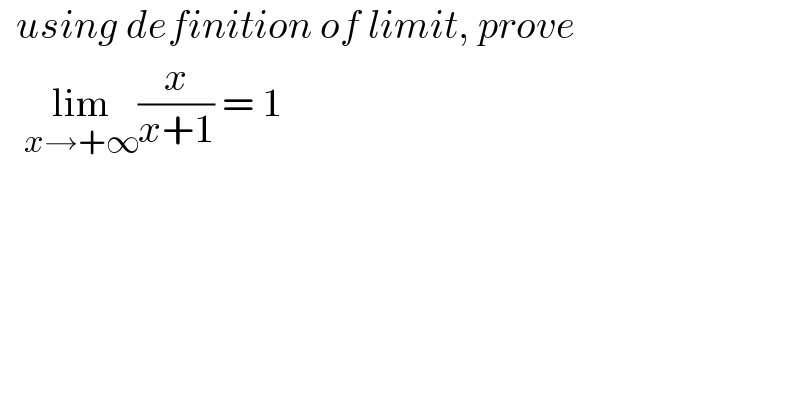
$$\:\:{using}\:{definition}\:{of}\:{limit},\:{prove}\: \\ $$$$\:\:\:\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\frac{{x}}{{x}+\mathrm{1}}\:=\:\mathrm{1} \\ $$
Answered by ERLY last updated on 27/Aug/23

$${tu}\:{appliques}\:{le}\:{monome}\:{de}\:{plus}\:{haut}\:{degre}\:{tu}\:{aura}\:{lim}\:{x}/{x}\:{ce}\:{qui}\:{donne}\:\mathrm{1}\:\:\:\:\:\:{Erly}\:{rolvinst} \\ $$
