
Question Number 196496 by RoseAli last updated on 26/Aug/23
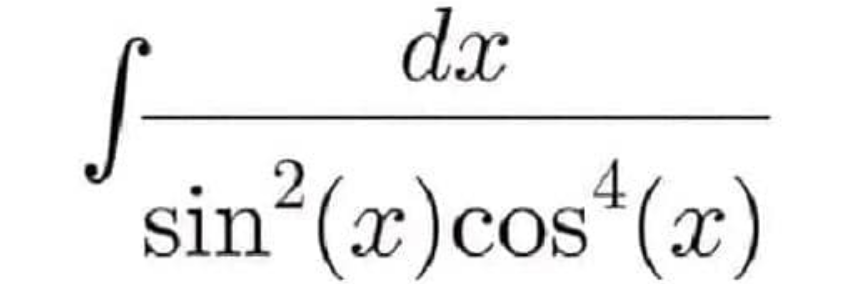
Answered by witcher3 last updated on 26/Aug/23
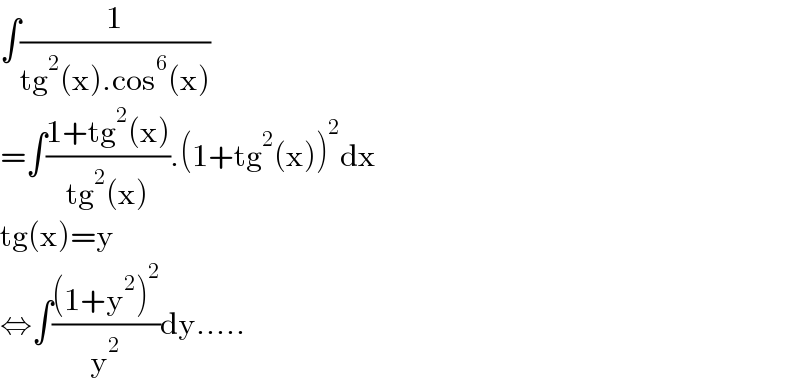
$$\int\frac{\mathrm{1}}{\mathrm{tg}^{\mathrm{2}} \left(\mathrm{x}\right).\mathrm{cos}^{\mathrm{6}} \left(\mathrm{x}\right)} \\ $$$$=\int\frac{\mathrm{1}+\mathrm{tg}^{\mathrm{2}} \left(\mathrm{x}\right)}{\mathrm{tg}^{\mathrm{2}} \left(\mathrm{x}\right)}.\left(\mathrm{1}+\mathrm{tg}^{\mathrm{2}} \left(\mathrm{x}\right)\right)^{\mathrm{2}} \mathrm{dx} \\ $$$$\mathrm{tg}\left(\mathrm{x}\right)=\mathrm{y} \\ $$$$\Leftrightarrow\int\frac{\left(\mathrm{1}+\mathrm{y}^{\mathrm{2}} \right)^{\mathrm{2}} }{\mathrm{y}^{\mathrm{2}} }\mathrm{dy}..... \\ $$
Commented by York12 last updated on 26/Aug/23

$${Sir}\:{What}\:{Calculus}\:{book}\:{do}\:{you}\:{recommend} \\ $$$${For}\:{Theory}\:{And}\:{problems} \\ $$
