
Question Number 196467 by sonukgindia last updated on 25/Aug/23
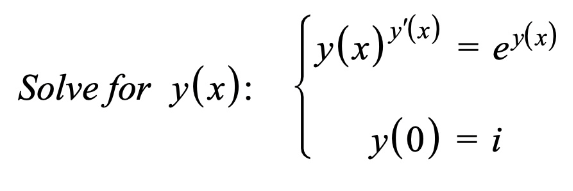
Answered by mr W last updated on 25/Aug/23
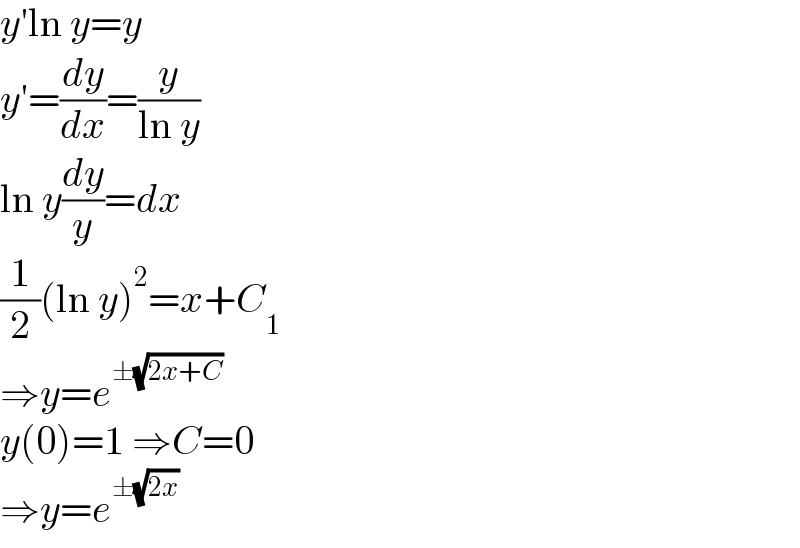
$${y}'\mathrm{ln}\:{y}={y} \\ $$$${y}'=\frac{{dy}}{{dx}}=\frac{{y}}{\mathrm{ln}\:{y}} \\ $$$$\mathrm{ln}\:{y}\frac{{dy}}{{y}}={dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{ln}\:{y}\right)^{\mathrm{2}} ={x}+{C}_{\mathrm{1}} \\ $$$$\Rightarrow{y}={e}^{\pm\sqrt{\mathrm{2}{x}+{C}}} \\ $$$${y}\left(\mathrm{0}\right)=\mathrm{1}\:\Rightarrow{C}=\mathrm{0} \\ $$$$\Rightarrow{y}={e}^{\pm\sqrt{\mathrm{2}{x}}} \\ $$
Commented by mahdipoor last updated on 31/Aug/23
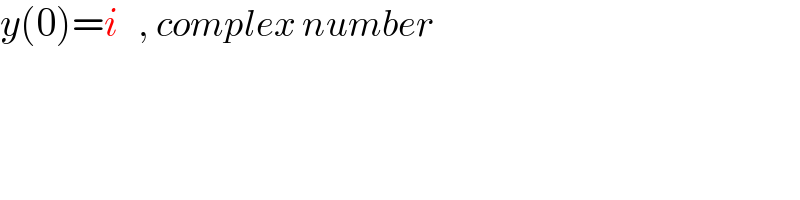
$${y}\left(\mathrm{0}\right)={i}\:\:\:,\:{complex}\:{number} \\ $$
Commented by mr W last updated on 25/Aug/23

$${y}\left(\mathrm{0}\right)={i}\:{is}\:{non}−{sense}\:{to}\:{me},\:{so}\:{i} \\ $$$${assumed}\:{y}\left(\mathrm{0}\right)=\mathrm{1}\:{is}\:{meant}. \\ $$
