
Question Number 196401 by RoseAli last updated on 24/Aug/23

$$\mathrm{if}\:{y}=\mathrm{sin}\:{x}\: \\ $$$$\mathrm{find}\:\frac{\boldsymbol{{d}}^{\mathrm{2}} }{\boldsymbol{{d}}{y}^{\mathrm{2}} }\mathrm{co}\boldsymbol{{s}}^{\mathrm{7}} \boldsymbol{{x}} \\ $$
Answered by qaz last updated on 24/Aug/23
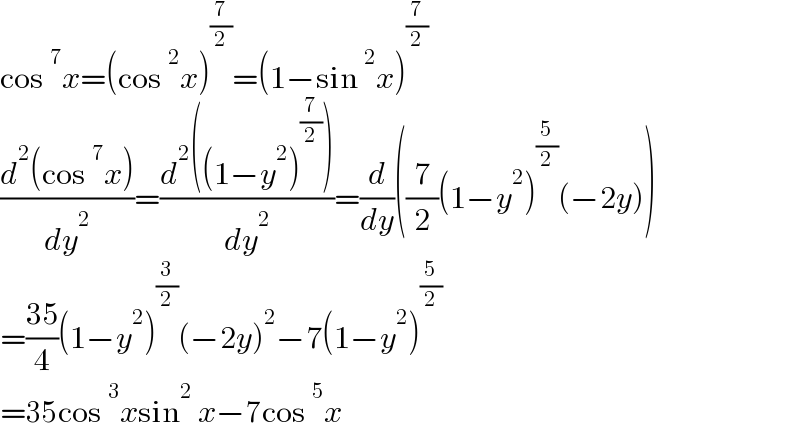
$$\mathrm{cos}\:^{\mathrm{7}} {x}=\left(\mathrm{cos}\:^{\mathrm{2}} {x}\right)^{\frac{\mathrm{7}}{\mathrm{2}}} =\left(\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} {x}\right)^{\frac{\mathrm{7}}{\mathrm{2}}} \\ $$$$\frac{{d}^{\mathrm{2}} \left(\mathrm{cos}\:^{\mathrm{7}} {x}\right)}{{dy}^{\mathrm{2}} }=\frac{{d}^{\mathrm{2}} \left(\left(\mathrm{1}−{y}^{\mathrm{2}} \right)^{\frac{\mathrm{7}}{\mathrm{2}}} \right)}{{dy}^{\mathrm{2}} }=\frac{{d}}{{dy}}\left(\frac{\mathrm{7}}{\mathrm{2}}\left(\mathrm{1}−{y}^{\mathrm{2}} \right)^{\frac{\mathrm{5}}{\mathrm{2}}} \left(−\mathrm{2}{y}\right)\right) \\ $$$$=\frac{\mathrm{35}}{\mathrm{4}}\left(\mathrm{1}−{y}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} \left(−\mathrm{2}{y}\right)^{\mathrm{2}} −\mathrm{7}\left(\mathrm{1}−{y}^{\mathrm{2}} \right)^{\frac{\mathrm{5}}{\mathrm{2}}} \\ $$$$=\mathrm{35cos}\:^{\mathrm{3}} {x}\mathrm{sin}^{\mathrm{2}} \:{x}−\mathrm{7cos}\:^{\mathrm{5}} {x} \\ $$
Answered by mr W last updated on 24/Aug/23
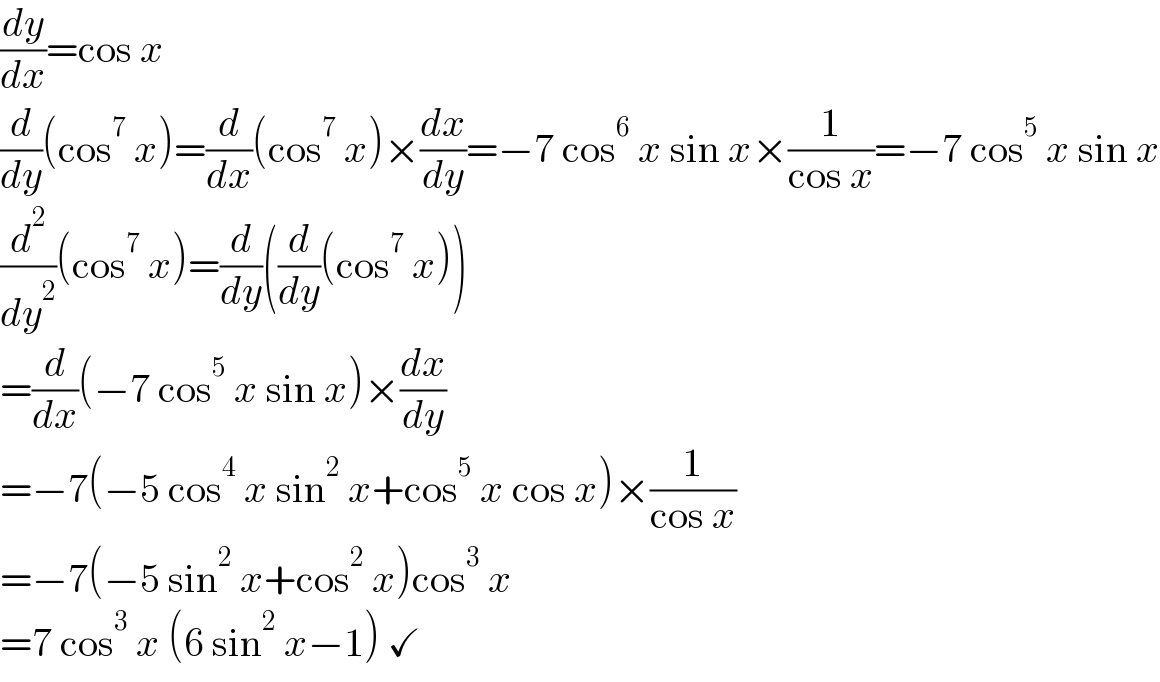
$$\frac{{dy}}{{dx}}=\mathrm{cos}\:{x} \\ $$$$\frac{{d}}{{dy}}\left(\mathrm{cos}^{\mathrm{7}} \:{x}\right)=\frac{{d}}{{dx}}\left(\mathrm{cos}^{\mathrm{7}} \:{x}\right)×\frac{{dx}}{{dy}}=−\mathrm{7}\:\mathrm{cos}^{\mathrm{6}} \:{x}\:\mathrm{sin}\:{x}×\frac{\mathrm{1}}{\mathrm{cos}\:{x}}=−\mathrm{7}\:\mathrm{cos}^{\mathrm{5}} \:{x}\:\mathrm{sin}\:{x} \\ $$$$\frac{{d}^{\mathrm{2}} }{{dy}^{\mathrm{2}} }\left(\mathrm{cos}^{\mathrm{7}} \:{x}\right)=\frac{{d}}{{dy}}\left(\frac{{d}}{{dy}}\left(\mathrm{cos}^{\mathrm{7}} \:{x}\right)\right) \\ $$$$=\frac{{d}}{{dx}}\left(−\mathrm{7}\:\mathrm{cos}^{\mathrm{5}} \:{x}\:\mathrm{sin}\:{x}\right)×\frac{{dx}}{{dy}} \\ $$$$=−\mathrm{7}\left(−\mathrm{5}\:\mathrm{cos}^{\mathrm{4}} \:{x}\:\mathrm{sin}^{\mathrm{2}} \:{x}+\mathrm{cos}^{\mathrm{5}} \:{x}\:\mathrm{cos}\:{x}\right)×\frac{\mathrm{1}}{\mathrm{cos}\:{x}} \\ $$$$=−\mathrm{7}\left(−\mathrm{5}\:\mathrm{sin}^{\mathrm{2}} \:{x}+\mathrm{cos}^{\mathrm{2}} \:{x}\right)\mathrm{cos}^{\mathrm{3}} \:{x} \\ $$$$=\mathrm{7}\:\mathrm{cos}^{\mathrm{3}} \:{x}\:\left(\mathrm{6}\:\mathrm{sin}^{\mathrm{2}} \:{x}−\mathrm{1}\right)\:\checkmark \\ $$
Answered by cortano12 last updated on 24/Aug/23
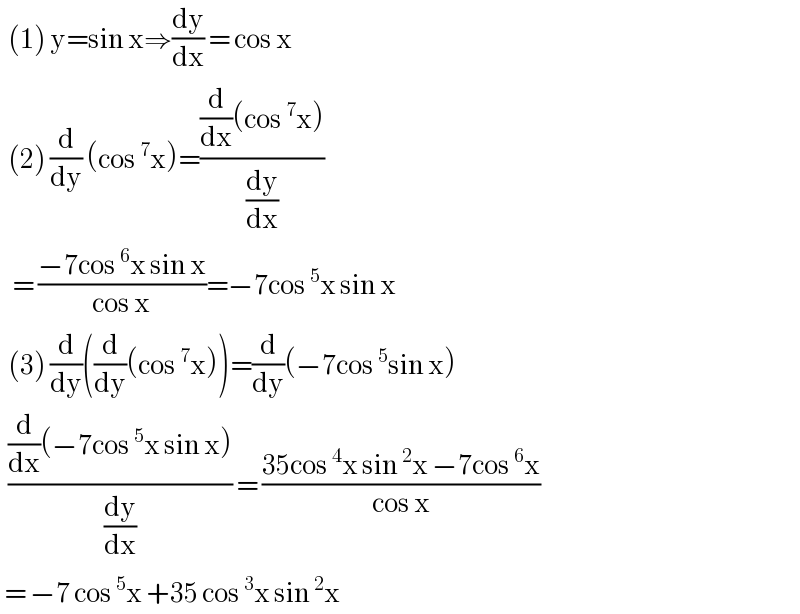
$$\:\:\left(\mathrm{1}\right)\:\mathrm{y}=\mathrm{sin}\:\mathrm{x}\Rightarrow\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\mathrm{cos}\:\mathrm{x} \\ $$$$\:\:\left(\mathrm{2}\right)\:\frac{\mathrm{d}}{\mathrm{dy}}\:\left(\mathrm{cos}\:^{\mathrm{7}} \mathrm{x}\right)=\frac{\frac{\mathrm{d}}{\mathrm{dx}}\left(\mathrm{cos}\:^{\mathrm{7}} \mathrm{x}\right)}{\frac{\mathrm{dy}}{\mathrm{dx}}} \\ $$$$\:\:\:=\:\frac{−\mathrm{7cos}\:^{\mathrm{6}} \mathrm{x}\:\mathrm{sin}\:\mathrm{x}}{\mathrm{cos}\:\mathrm{x}}=−\mathrm{7cos}\:^{\mathrm{5}} \mathrm{x}\:\mathrm{sin}\:\mathrm{x} \\ $$$$\:\:\left(\mathrm{3}\right)\:\frac{\mathrm{d}}{\mathrm{dy}}\left(\frac{\mathrm{d}}{\mathrm{dy}}\left(\mathrm{cos}\:^{\mathrm{7}} \mathrm{x}\right)\right)=\frac{\mathrm{d}}{\mathrm{dy}}\left(−\mathrm{7cos}\:^{\mathrm{5}} \mathrm{sin}\:\mathrm{x}\right) \\ $$$$\:\:\frac{\frac{\mathrm{d}}{\mathrm{dx}}\left(−\mathrm{7cos}\:^{\mathrm{5}} \mathrm{x}\:\mathrm{sin}\:\mathrm{x}\right)}{\frac{\mathrm{dy}}{\mathrm{dx}}}\:=\:\frac{\mathrm{35cos}\:^{\mathrm{4}} \mathrm{x}\:\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}\:−\mathrm{7cos}\:^{\mathrm{6}} \mathrm{x}}{\mathrm{cos}\:\mathrm{x}} \\ $$$$\:=\:−\mathrm{7}\:\mathrm{cos}\:^{\mathrm{5}} \mathrm{x}\:+\mathrm{35}\:\mathrm{cos}\:^{\mathrm{3}} \mathrm{x}\:\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}\: \\ $$
