
Question Number 196388 by sonukgindia last updated on 24/Aug/23

Answered by deleteduser1 last updated on 24/Aug/23
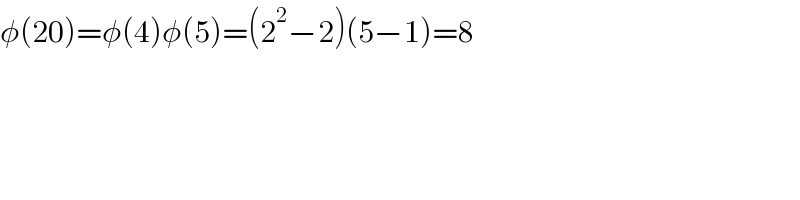
$$\phi\left(\mathrm{20}\right)=\phi\left(\mathrm{4}\right)\phi\left(\mathrm{5}\right)=\left(\mathrm{2}^{\mathrm{2}} −\mathrm{2}\right)\left(\mathrm{5}−\mathrm{1}\right)=\mathrm{8} \\ $$
Answered by BaliramKumar last updated on 24/Aug/23
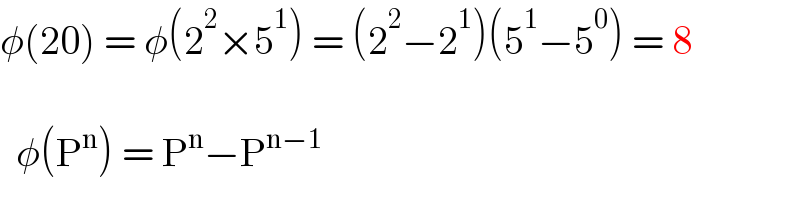
$$\phi\left(\mathrm{20}\right)\:=\:\phi\left(\mathrm{2}^{\mathrm{2}} ×\mathrm{5}^{\mathrm{1}} \right)\:=\:\left(\mathrm{2}^{\mathrm{2}} −\mathrm{2}^{\mathrm{1}} \right)\left(\mathrm{5}^{\mathrm{1}} −\mathrm{5}^{\mathrm{0}} \right)\:=\:\mathrm{8} \\ $$$$ \\ $$$$\begin{array}{|c|}{\phi\left(\mathrm{P}^{\mathrm{n}} \right)\:=\:\mathrm{P}^{\mathrm{n}} −\mathrm{P}^{\mathrm{n}−\mathrm{1}} }\\\hline\end{array} \\ $$
