
Question Number 196375 by RoseAli last updated on 23/Aug/23

$$\int\frac{{dx}}{{x}\left({x}^{\mathrm{4}} −\mathrm{1}\right)} \\ $$
Commented by RoseAli last updated on 23/Aug/23

$$\int\frac{{dx}}{{x}\left({x}^{\mathrm{4}} +\mathrm{1}\right)} \\ $$
Answered by MM42 last updated on 23/Aug/23
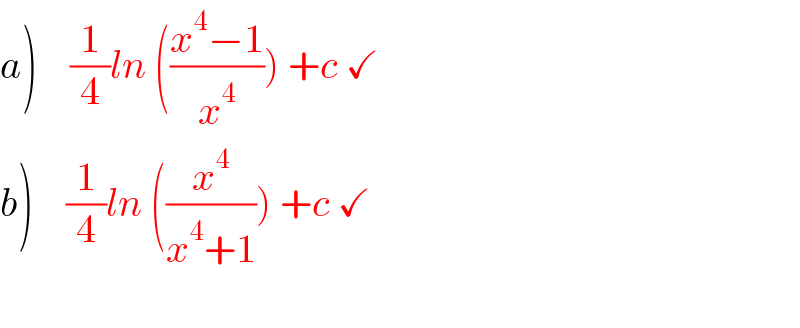
$$\left.{a}\right)\:\:\:\:\frac{\mathrm{1}}{\mathrm{4}}{ln}\:\left(\frac{{x}^{\mathrm{4}} −\mathrm{1}}{{x}^{\mathrm{4}} }\right)\:+{c}\:\checkmark \\ $$$$\left.{b}\right)\:\:\:\:\frac{\mathrm{1}}{\mathrm{4}}{ln}\:\left(\frac{{x}^{\mathrm{4}} }{{x}^{\mathrm{4}} +\mathrm{1}}\right)\:+{c}\:\checkmark \\ $$$$ \\ $$
Commented by RoseAli last updated on 23/Aug/23

$$\mathrm{step}\:\mathrm{by}\:\mathrm{step} \\ $$
Commented by Frix last updated on 23/Aug/23
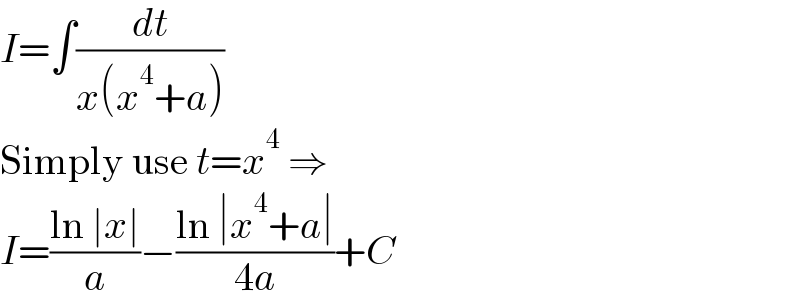
$${I}=\int\frac{{dt}}{{x}\left({x}^{\mathrm{4}} +{a}\right)} \\ $$$$\mathrm{Simply}\:\mathrm{use}\:{t}={x}^{\mathrm{4}} \:\Rightarrow \\ $$$${I}=\frac{\mathrm{ln}\:\mid{x}\mid}{{a}}−\frac{\mathrm{ln}\:\mid{x}^{\mathrm{4}} +{a}\mid}{\mathrm{4}{a}}+{C} \\ $$
Commented by MM42 last updated on 24/Aug/23
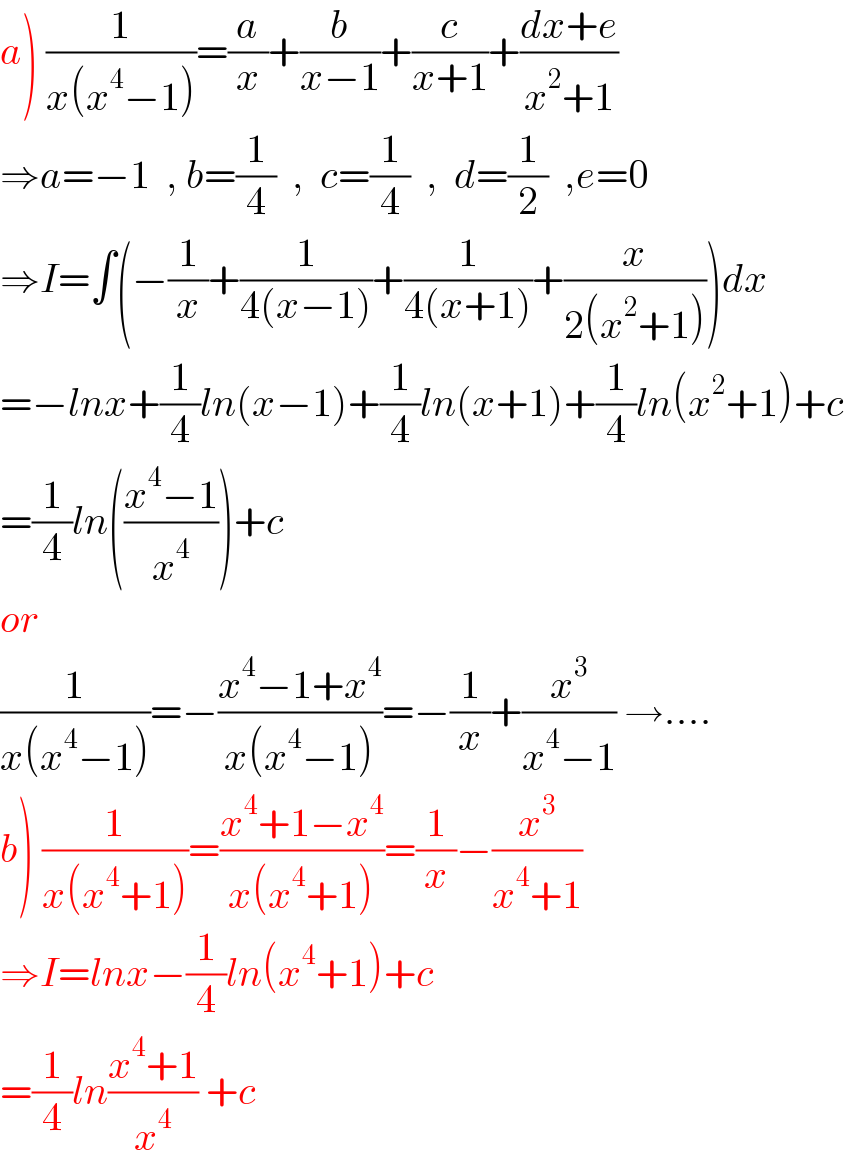
$$\left.{a}\right)\:\frac{\mathrm{1}}{{x}\left({x}^{\mathrm{4}} −\mathrm{1}\right)}=\frac{{a}}{{x}}+\frac{{b}}{{x}−\mathrm{1}}+\frac{{c}}{{x}+\mathrm{1}}+\frac{{dx}+{e}}{{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\Rightarrow{a}=−\mathrm{1}\:\:,\:{b}=\frac{\mathrm{1}}{\mathrm{4}}\:\:,\:\:{c}=\frac{\mathrm{1}}{\mathrm{4}}\:\:,\:\:{d}=\frac{\mathrm{1}}{\mathrm{2}}\:\:,{e}=\mathrm{0} \\ $$$$\Rightarrow{I}=\int\left(−\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{\mathrm{4}\left({x}−\mathrm{1}\right)}+\frac{\mathrm{1}}{\mathrm{4}\left({x}+\mathrm{1}\right)}+\frac{{x}}{\mathrm{2}\left({x}^{\mathrm{2}} +\mathrm{1}\right)}\right){dx} \\ $$$$=−{lnx}+\frac{\mathrm{1}}{\mathrm{4}}{ln}\left({x}−\mathrm{1}\right)+\frac{\mathrm{1}}{\mathrm{4}}{ln}\left({x}+\mathrm{1}\right)+\frac{\mathrm{1}}{\mathrm{4}}{ln}\left({x}^{\mathrm{2}} +\mathrm{1}\right)+{c} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}{ln}\left(\frac{{x}^{\mathrm{4}} −\mathrm{1}}{{x}^{\mathrm{4}} }\right)+{c} \\ $$$${or}\: \\ $$$$\frac{\mathrm{1}}{{x}\left({x}^{\mathrm{4}} −\mathrm{1}\right)}=−\frac{{x}^{\mathrm{4}} −\mathrm{1}+{x}^{\mathrm{4}} }{{x}\left({x}^{\mathrm{4}} −\mathrm{1}\right)}=−\frac{\mathrm{1}}{{x}}+\frac{{x}^{\mathrm{3}} }{{x}^{\mathrm{4}} −\mathrm{1}}\:\rightarrow.... \\ $$$$\left.{b}\right)\:\frac{\mathrm{1}}{{x}\left({x}^{\mathrm{4}} +\mathrm{1}\right)}=\frac{{x}^{\mathrm{4}} +\mathrm{1}−{x}^{\mathrm{4}} }{{x}\left({x}^{\mathrm{4}} +\mathrm{1}\right)}=\frac{\mathrm{1}}{{x}}−\frac{{x}^{\mathrm{3}} }{{x}^{\mathrm{4}} +\mathrm{1}} \\ $$$$\Rightarrow{I}={lnx}−\frac{\mathrm{1}}{\mathrm{4}}{ln}\left({x}^{\mathrm{4}} +\mathrm{1}\right)+{c} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}{ln}\frac{{x}^{\mathrm{4}} +\mathrm{1}}{{x}^{\mathrm{4}} }\:+{c}\: \\ $$
