
Question Number 196360 by mathlove last updated on 23/Aug/23
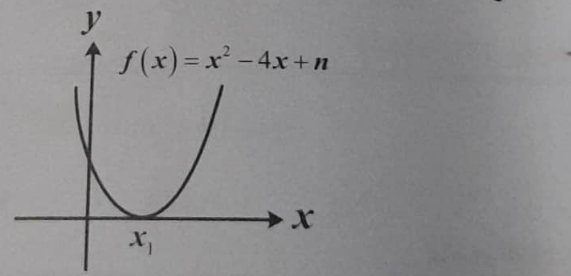
Commented by mathlove last updated on 23/Aug/23

$${x}_{\mathrm{1}} +{n}=? \\ $$
Answered by deleteduser1 last updated on 23/Aug/23
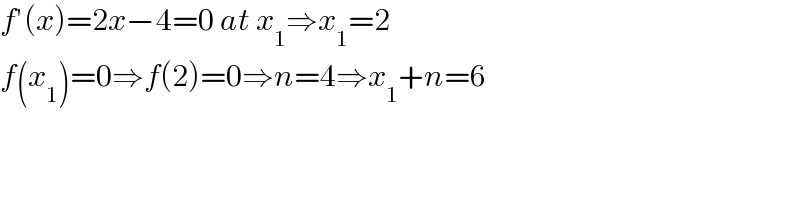
$${f}'\left({x}\right)=\mathrm{2}{x}−\mathrm{4}=\mathrm{0}\:{at}\:{x}_{\mathrm{1}} \Rightarrow{x}_{\mathrm{1}} =\mathrm{2} \\ $$$${f}\left({x}_{\mathrm{1}} \right)=\mathrm{0}\Rightarrow{f}\left(\mathrm{2}\right)=\mathrm{0}\Rightarrow{n}=\mathrm{4}\Rightarrow{x}_{\mathrm{1}} +{n}=\mathrm{6} \\ $$
Commented by mathlove last updated on 23/Aug/23

$${thanks} \\ $$
Answered by mr W last updated on 23/Aug/23
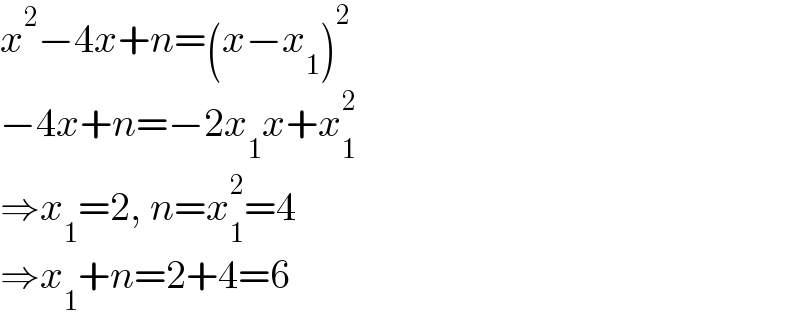
$${x}^{\mathrm{2}} −\mathrm{4}{x}+{n}=\left({x}−{x}_{\mathrm{1}} \right)^{\mathrm{2}} \\ $$$$−\mathrm{4}{x}+{n}=−\mathrm{2}{x}_{\mathrm{1}} {x}+{x}_{\mathrm{1}} ^{\mathrm{2}} \\ $$$$\Rightarrow{x}_{\mathrm{1}} =\mathrm{2},\:{n}={x}_{\mathrm{1}} ^{\mathrm{2}} =\mathrm{4} \\ $$$$\Rightarrow{x}_{\mathrm{1}} +{n}=\mathrm{2}+\mathrm{4}=\mathrm{6} \\ $$
