Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 196275 by AROUNAMoussa last updated on 21/Aug/23

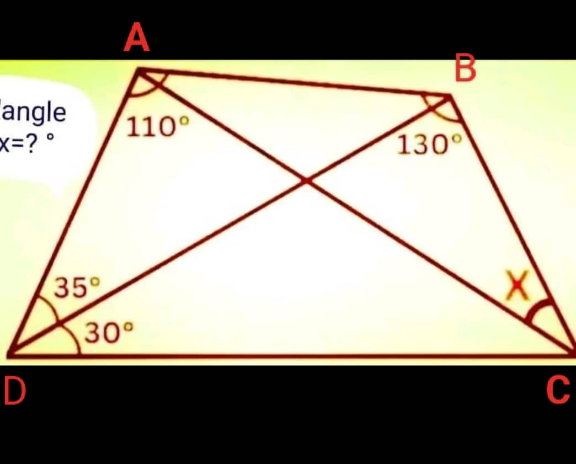
Answered by MM42 last updated on 21/Aug/23

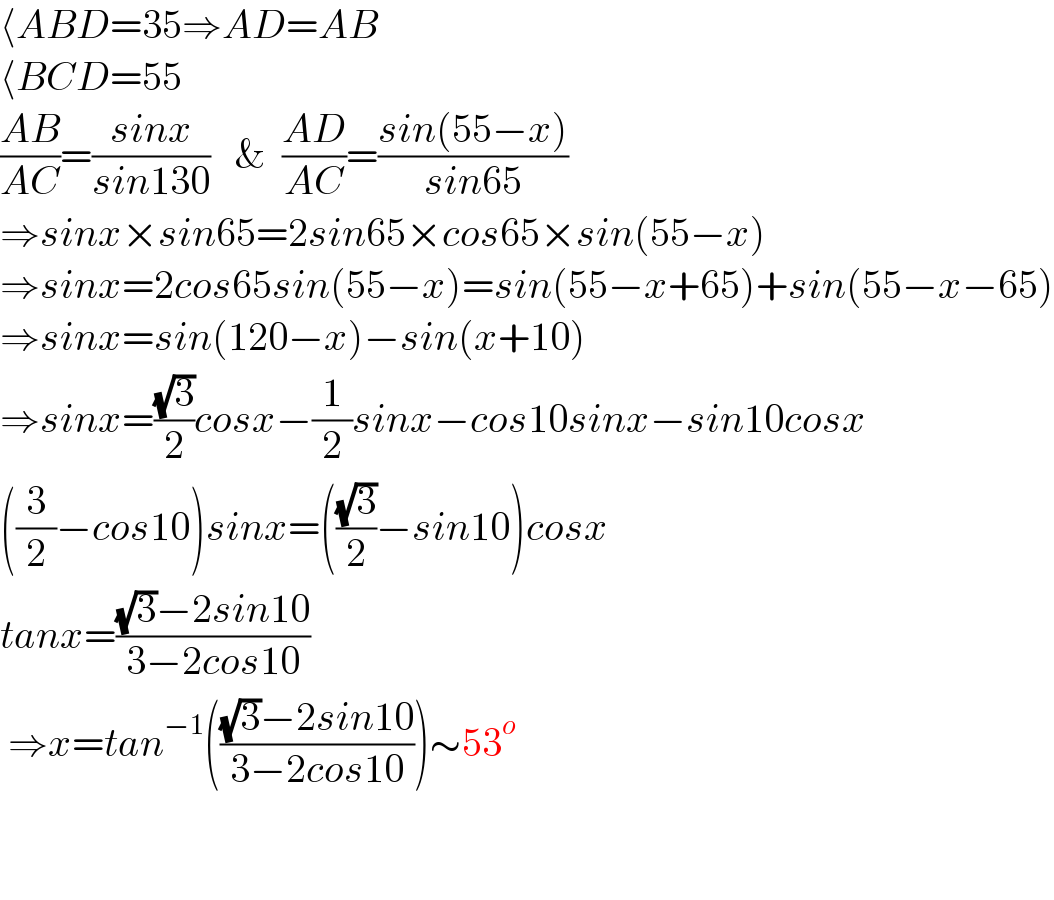
⟨ABD=35⇒AD=AB ⟨BCD=55 ((AB)/(AC))=((sinx)/(sin130)) & ((AD)/(AC))=((sin(55−x))/(sin65)) ⇒sinx×sin65=2sin65×cos65×sin(55−x) ⇒sinx=2cos65sin(55−x)=sin(55−x+65)+sin(55−x−65) ⇒sinx=sin(120−x)−sin(x+10) ⇒sinx=((√3)/2)cosx−(1/2)sinx−cos10sinx−sin10cosx ((3/2)−cos10)sinx=(((√3)/2)−sin10)cosx tanx=(((√3)−2sin10)/(3−2cos10)) ⇒x=tan^(−1) ((((√3)−2sin10)/(3−2cos10)))∼53^o

$$\langle{ABD}=\mathrm{35}\Rightarrow{AD}={AB} \\ $$$$\langle{BCD}=\mathrm{55} \\ $$$$\frac{{AB}}{{AC}}=\frac{{sinx}}{{sin}\mathrm{130}}\:\:\:\&\:\:\frac{{AD}}{{AC}}=\frac{{sin}\left(\mathrm{55}−{x}\right)}{{sin}\mathrm{65}} \\ $$$$\Rightarrow{sinx}×{sin}\mathrm{65}=\mathrm{2}{sin}\mathrm{65}×{cos}\mathrm{65}×{sin}\left(\mathrm{55}−{x}\right) \\ $$$$\Rightarrow{sinx}=\mathrm{2}{cos}\mathrm{65}{sin}\left(\mathrm{55}−{x}\right)={sin}\left(\mathrm{55}−{x}+\mathrm{65}\right)+{sin}\left(\mathrm{55}−{x}−\mathrm{65}\right) \\ $$$$\Rightarrow{sinx}={sin}\left(\mathrm{120}−{x}\right)−{sin}\left({x}+\mathrm{10}\right) \\ $$$$\Rightarrow{sinx}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{cosx}−\frac{\mathrm{1}}{\mathrm{2}}{sinx}−{cos}\mathrm{10}{sinx}−{sin}\mathrm{10}{cosx} \\ $$$$\left(\frac{\mathrm{3}}{\mathrm{2}}−{cos}\mathrm{10}\right){sinx}=\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−{sin}\mathrm{10}\right){cosx} \\ $$$${tanx}=\frac{\sqrt{\mathrm{3}}−\mathrm{2}{sin}\mathrm{10}}{\mathrm{3}−\mathrm{2}{cos}\mathrm{10}} \\ $$$$\:\Rightarrow{x}={tan}^{−\mathrm{1}} \left(\frac{\sqrt{\mathrm{3}}−\mathrm{2}{sin}\mathrm{10}}{\mathrm{3}−\mathrm{2}{cos}\mathrm{10}}\right)\sim\mathrm{53}^{{o}} \\ $$$$ \\ $$$$ \\ $$

Commented by AROUNAMoussa last updated on 21/Aug/23

Merci bcp !

$${Merci}\:{bcp}\:! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com