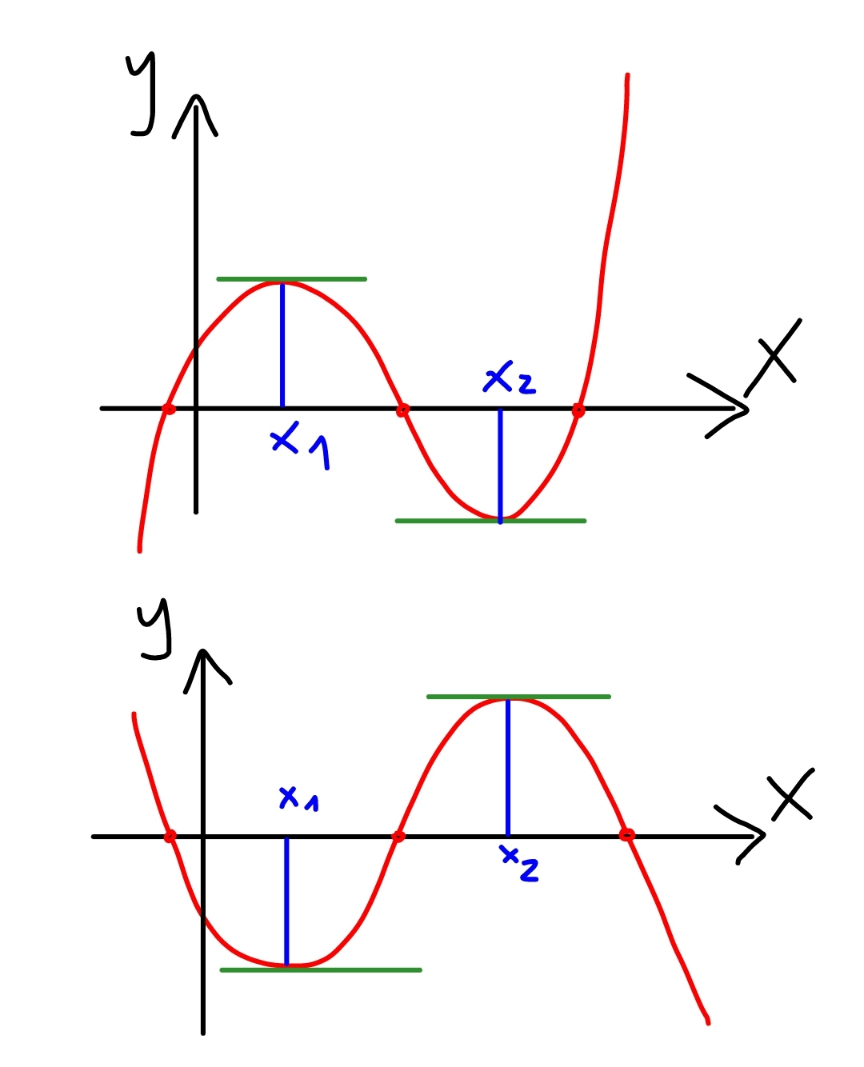
Question Number 196183 by cortano12 last updated on 19/Aug/23
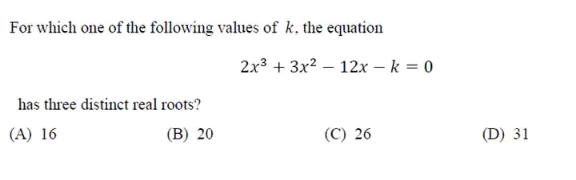
Answered by dimentri last updated on 19/Aug/23

$$\: \\ $$$$ \\ $$$$ \\ $$$$ {f}\left({x}\right)={ax}^{\mathrm{3}} +{bx}^{\mathrm{2}} +{cx}+{d}\: \\ $$$$\:\: \\ $$$$ \bigtriangleup^{\mathrm{2}} =\:\left({bc}\right)^{\mathrm{2}} −\mathrm{4}\left({ac}^{\mathrm{3}} +{b}^{\mathrm{3}} {d}\right)−\mathrm{9}{ad}\left(\mathrm{3}{ad}−\mathrm{2}{bc}\right)>\mathrm{0} \\ $$$$\:\: \\ $$$$ \\ $$$$ \mathrm{36}^{\mathrm{2}} +\mathrm{4}\left(\mathrm{12}^{\mathrm{3}} .\mathrm{2}+\mathrm{3}^{\mathrm{3}} {k}\right)+\mathrm{18}{k}\left(\mathrm{72}−\mathrm{6}{k}\right)>\mathrm{0} \\ $$$$\:\:{k}^{\mathrm{2}} −\mathrm{13}{k}−\mathrm{140}<\mathrm{0} \\ $$$$\:\:\left({k}−\mathrm{20}\right)\left({k}+\mathrm{7}\right)<\mathrm{0} \\ $$$$\:\:−\mathrm{7}<{k}<\mathrm{20} \\ $$$$\:\:\:{Answer}\::\:{A} \\ $$
Answered by mr W last updated on 19/Aug/23
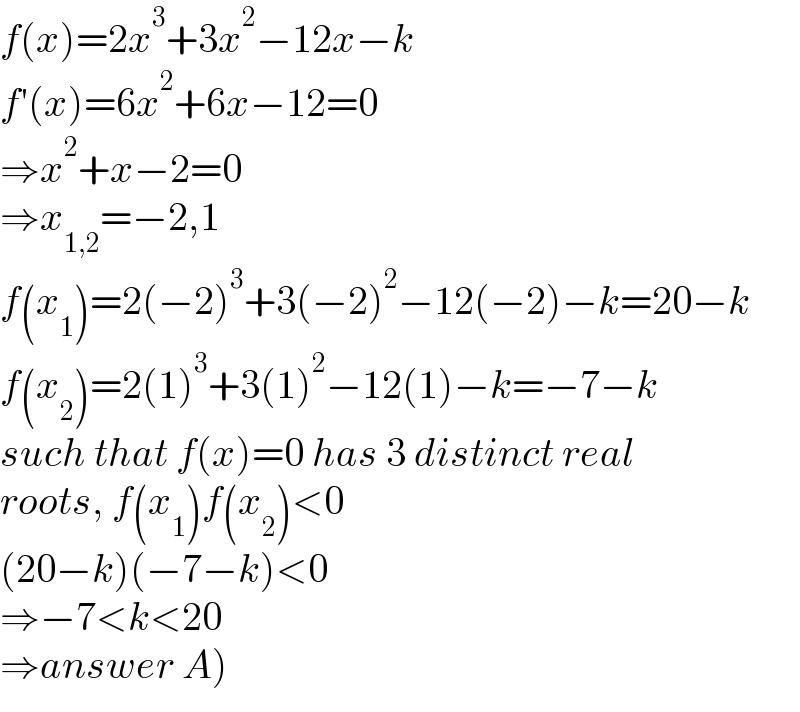
$${f}\left({x}\right)=\mathrm{2}{x}^{\mathrm{3}} +\mathrm{3}{x}^{\mathrm{2}} −\mathrm{12}{x}−{k} \\ $$$${f}'\left({x}\right)=\mathrm{6}{x}^{\mathrm{2}} +\mathrm{6}{x}−\mathrm{12}=\mathrm{0} \\ $$$$\Rightarrow{x}^{\mathrm{2}} +{x}−\mathrm{2}=\mathrm{0} \\ $$$$\Rightarrow{x}_{\mathrm{1},\mathrm{2}} =−\mathrm{2},\mathrm{1} \\ $$$${f}\left({x}_{\mathrm{1}} \right)=\mathrm{2}\left(−\mathrm{2}\right)^{\mathrm{3}} +\mathrm{3}\left(−\mathrm{2}\right)^{\mathrm{2}} −\mathrm{12}\left(−\mathrm{2}\right)−{k}=\mathrm{20}−{k} \\ $$$${f}\left({x}_{\mathrm{2}} \right)=\mathrm{2}\left(\mathrm{1}\right)^{\mathrm{3}} +\mathrm{3}\left(\mathrm{1}\right)^{\mathrm{2}} −\mathrm{12}\left(\mathrm{1}\right)−{k}=−\mathrm{7}−{k} \\ $$$${such}\:{that}\:{f}\left({x}\right)=\mathrm{0}\:{has}\:\mathrm{3}\:{distinct}\:{real}\: \\ $$$${roots},\:{f}\left({x}_{\mathrm{1}} \right){f}\left({x}_{\mathrm{2}} \right)<\mathrm{0} \\ $$$$\left(\mathrm{20}−{k}\right)\left(−\mathrm{7}−{k}\right)<\mathrm{0} \\ $$$$\Rightarrow−\mathrm{7}<{k}<\mathrm{20} \\ $$$$\left.\Rightarrow{answer}\:{A}\right) \\ $$
Commented by mr W last updated on 19/Aug/23