
Question Number 196173 by pticantor last updated on 19/Aug/23
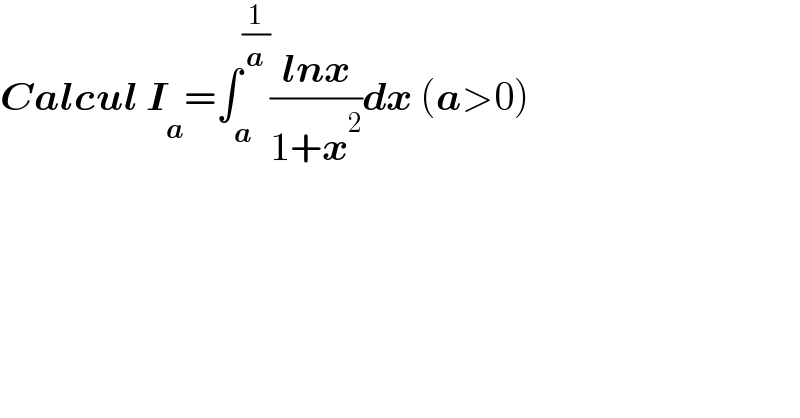
$$\boldsymbol{{Calcul}}\:\boldsymbol{{I}}_{\boldsymbol{{a}}} =\int_{\boldsymbol{{a}}} ^{\frac{\mathrm{1}}{\boldsymbol{{a}}}} \frac{\boldsymbol{{lnx}}}{\mathrm{1}+\boldsymbol{{x}}^{\mathrm{2}} }\boldsymbol{{dx}}\:\left(\boldsymbol{{a}}>\mathrm{0}\right)\: \\ $$
Answered by Erico last updated on 19/Aug/23
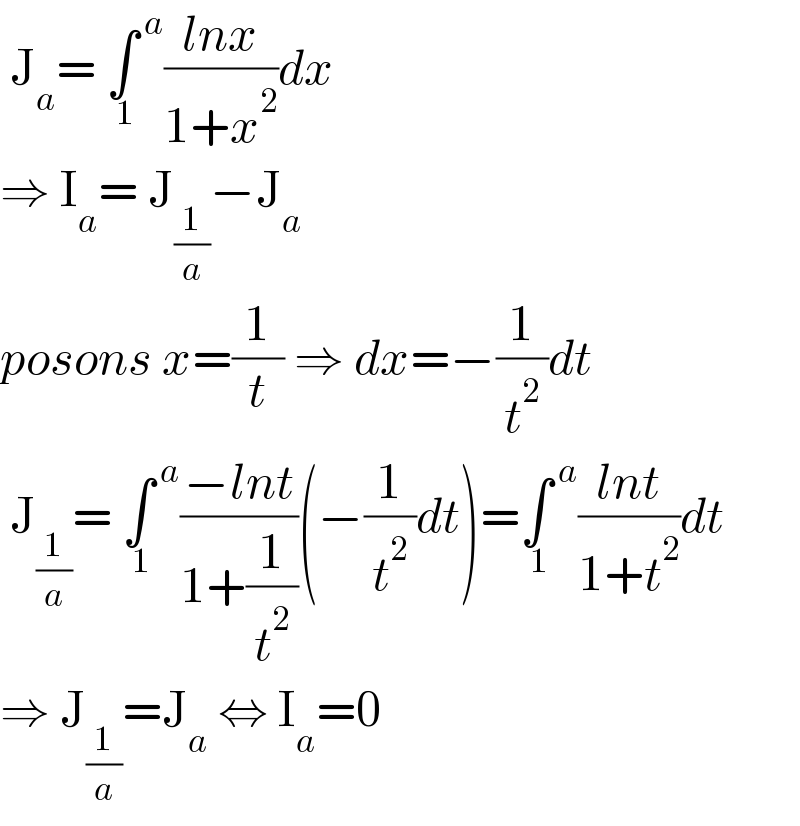
$$\:\mathrm{J}_{{a}} =\:\underset{\:\mathrm{1}} {\int}^{\:{a}} \frac{{lnx}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$$\Rightarrow\:\mathrm{I}_{{a}} =\:\mathrm{J}_{\frac{\mathrm{1}}{{a}}} −\mathrm{J}_{{a}} \\ $$$${posons}\:{x}=\frac{\mathrm{1}}{{t}}\:\Rightarrow\:{dx}=−\frac{\mathrm{1}}{{t}^{\mathrm{2}} }{dt} \\ $$$$\:\mathrm{J}_{\frac{\mathrm{1}}{{a}}} =\:\underset{\:\mathrm{1}} {\int}^{\:{a}} \frac{−{lnt}}{\mathrm{1}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }}\left(−\frac{\mathrm{1}}{{t}^{\mathrm{2}} }{dt}\right)=\underset{\:\mathrm{1}} {\int}^{\:{a}} \frac{{lnt}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$$$\Rightarrow\:\mathrm{J}_{\frac{\mathrm{1}}{{a}}} =\mathrm{J}_{{a}} \:\Leftrightarrow\:\mathrm{I}_{{a}} =\mathrm{0} \\ $$
