Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 196165 by mathlove last updated on 19/Aug/23

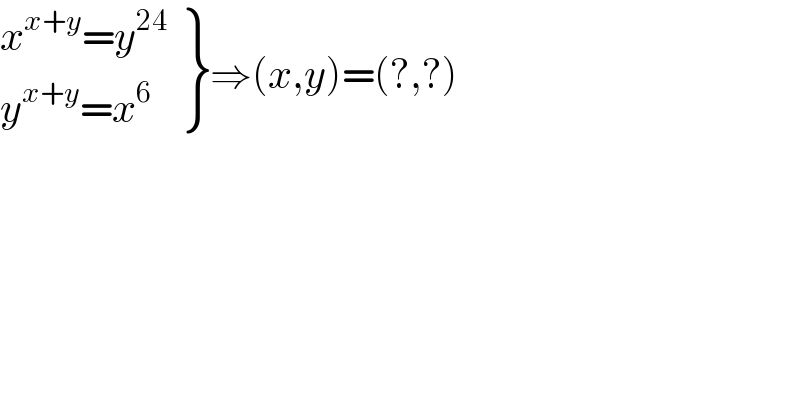
{: ((x^(x+y) =y^(24) )),((y^(x+y) =x^6 )) }⇒(x,y)=(?,?)

$$\left.\begin{matrix}{{x}^{{x}+{y}} ={y}^{\mathrm{24}} }\\{{y}^{{x}+{y}} ={x}^{\mathrm{6}} }\end{matrix}\right\}\Rightarrow\left({x},{y}\right)=\left(?,?\right) \\ $$

Answered by liuxinnan last updated on 19/Aug/23

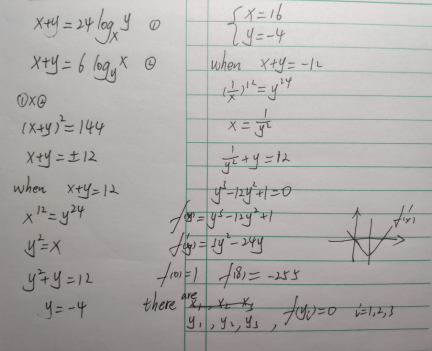
Answered by Frix last updated on 19/Aug/23

Obviously x+y=±12 We then get 1. x^(−12) =(x+12)^(24) ∧(x+12)^(−12) =x^6 ∨ 2. x^(12) =(x−12)^(24) ∧(x−12)^(12) =x^6 ⇒ 1.1. x^(−1) =−(x+12)^2 x^3 +24x^2 +144x+1=0 x≈−12.2853∨x≈−11.7077∨x≈−.00695250 1.2. x^(−1) =(x+12)^2 x^3 +24x^2 +144x−1=0 x≈.00693642∨x≈−12.0035±.288571i 2.1. x=−(x−12)^2 x^2 −23x+144=0 x=((23)/2)±((√(47))/2)i 2.2. x=(x−12)^2 x^2 −25x+144=0 x=9∨x=16 Solve these for x, then get y. All real and complex solution pairs are valid. The “nice” solutions are 2.2. x=9∧y=3 ∨ x=16∧y=−4

$$\mathrm{Obviously}\:{x}+{y}=\pm\mathrm{12} \\ $$$$\mathrm{We}\:\mathrm{then}\:\mathrm{get} \\ $$$$\mathrm{1}.\:{x}^{−\mathrm{12}} =\left({x}+\mathrm{12}\right)^{\mathrm{24}} \wedge\left({x}+\mathrm{12}\right)^{−\mathrm{12}} ={x}^{\mathrm{6}} \\ $$$$\vee \\ $$$$\mathrm{2}.\:{x}^{\mathrm{12}} =\left({x}−\mathrm{12}\right)^{\mathrm{24}} \wedge\left({x}−\mathrm{12}\right)^{\mathrm{12}} ={x}^{\mathrm{6}} \\ $$$$\Rightarrow \\ $$$$\mathrm{1}.\mathrm{1}.\:{x}^{−\mathrm{1}} =−\left({x}+\mathrm{12}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:{x}^{\mathrm{3}} +\mathrm{24}{x}^{\mathrm{2}} +\mathrm{144}{x}+\mathrm{1}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:{x}\approx−\mathrm{12}.\mathrm{2853}\vee{x}\approx−\mathrm{11}.\mathrm{7077}\vee{x}\approx−.\mathrm{00695250} \\ $$$$\mathrm{1}.\mathrm{2}.\:{x}^{−\mathrm{1}} =\left({x}+\mathrm{12}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:{x}^{\mathrm{3}} +\mathrm{24}{x}^{\mathrm{2}} +\mathrm{144}{x}−\mathrm{1}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:{x}\approx.\mathrm{00693642}\vee{x}\approx−\mathrm{12}.\mathrm{0035}\pm.\mathrm{288571i} \\ $$$$\mathrm{2}.\mathrm{1}.\:{x}=−\left({x}−\mathrm{12}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:{x}^{\mathrm{2}} −\mathrm{23}{x}+\mathrm{144}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:{x}=\frac{\mathrm{23}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{47}}}{\mathrm{2}}\mathrm{i} \\ $$$$\mathrm{2}.\mathrm{2}.\:{x}=\left({x}−\mathrm{12}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:{x}^{\mathrm{2}} −\mathrm{25}{x}+\mathrm{144}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:{x}=\mathrm{9}\vee{x}=\mathrm{16} \\ $$$$ \\ $$$$\mathrm{Solve}\:\mathrm{these}\:\mathrm{for}\:{x},\:\mathrm{then}\:\mathrm{get}\:{y}.\:\mathrm{All}\:\mathrm{real}\:\mathrm{and} \\ $$$$\mathrm{complex}\:\mathrm{solution}\:\mathrm{pairs}\:\mathrm{are}\:\mathrm{valid}. \\ $$$$\mathrm{The}\:``\mathrm{nice}''\:\mathrm{solutions}\:\mathrm{are} \\ $$$$\mathrm{2}.\mathrm{2}.\:{x}=\mathrm{9}\wedge{y}=\mathrm{3}\:\vee\:{x}=\mathrm{16}\wedge{y}=−\mathrm{4} \\ $$

Commented by mathlove last updated on 19/Aug/23

thanks

$${thanks} \\ $$

Answered by mr W last updated on 19/Aug/23

(x+y)ln x=24ln y ...(i) (x+y)ln y=6ln x ...(ii) (i)×(ii): (x+y)^2 =6×24 ⇒x+y=±12 case 1: x+y=12 ln x=2ln y ⇒x=y^2 ⇒y^2 +y−12=0 ⇒y=−4, 3 ⇒x=16, 9 case 2: x+y=−12 ⇒(1/x)=y^2 (1/y^2 )+y+12=0 (1/y)=((((√(257))−1)/2))^(1/3) −((((√(257))+1)/2))^(1/3) y=(1/( ((((√(257))−1)/2))^(1/3) −((((√(257))+1)/2))^(1/3) )) x=−12−(1/( ((((√(257))−1)/2))^(1/3) −((((√(257))+1)/2))^(1/3) )) summary: (x,y)=(16,−4),(9,3),(−12−(1/( ((((√(257))−1)/2))^(1/3) −((((√(257))+1)/2))^(1/3) )),(1/( ((((√(257))−1)/2))^(1/3) −((((√(257))+1)/2))^(1/3) )))

$$\left({x}+{y}\right)\mathrm{ln}\:{x}=\mathrm{24ln}\:{y}\:\:\:...\left({i}\right) \\ $$$$\left({x}+{y}\right)\mathrm{ln}\:{y}=\mathrm{6ln}\:{x}\:\:\:...\left({ii}\right) \\ $$$$\left({i}\right)×\left({ii}\right): \\ $$$$\left({x}+{y}\right)^{\mathrm{2}} =\mathrm{6}×\mathrm{24} \\ $$$$\Rightarrow{x}+{y}=\pm\mathrm{12} \\ $$$${case}\:\mathrm{1}:\:{x}+{y}=\mathrm{12} \\ $$$$\mathrm{ln}\:{x}=\mathrm{2ln}\:{y} \\ $$$$\Rightarrow{x}={y}^{\mathrm{2}} \\ $$$$\Rightarrow{y}^{\mathrm{2}} +{y}−\mathrm{12}=\mathrm{0} \\ $$$$\Rightarrow{y}=−\mathrm{4},\:\mathrm{3}\:\Rightarrow{x}=\mathrm{16},\:\mathrm{9} \\ $$$${case}\:\mathrm{2}:\:{x}+{y}=−\mathrm{12} \\ $$$$\Rightarrow\frac{\mathrm{1}}{{x}}={y}^{\mathrm{2}} \\ $$$$\:\frac{\mathrm{1}}{{y}^{\mathrm{2}} }+{y}+\mathrm{12}=\mathrm{0} \\ $$$$\frac{\mathrm{1}}{{y}}=\sqrt[{\mathrm{3}}]{\frac{\sqrt{\mathrm{257}}−\mathrm{1}}{\mathrm{2}}}−\sqrt[{\mathrm{3}}]{\frac{\sqrt{\mathrm{257}}+\mathrm{1}}{\mathrm{2}}} \\ $$$${y}=\frac{\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{\frac{\sqrt{\mathrm{257}}−\mathrm{1}}{\mathrm{2}}}−\sqrt[{\mathrm{3}}]{\frac{\sqrt{\mathrm{257}}+\mathrm{1}}{\mathrm{2}}}} \\ $$$${x}=−\mathrm{12}−\frac{\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{\frac{\sqrt{\mathrm{257}}−\mathrm{1}}{\mathrm{2}}}−\sqrt[{\mathrm{3}}]{\frac{\sqrt{\mathrm{257}}+\mathrm{1}}{\mathrm{2}}}} \\ $$$${summary}: \\ $$$$\left({x},{y}\right)=\left(\mathrm{16},−\mathrm{4}\right),\left(\mathrm{9},\mathrm{3}\right),\left(−\mathrm{12}−\frac{\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{\frac{\sqrt{\mathrm{257}}−\mathrm{1}}{\mathrm{2}}}−\sqrt[{\mathrm{3}}]{\frac{\sqrt{\mathrm{257}}+\mathrm{1}}{\mathrm{2}}}},\frac{\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{\frac{\sqrt{\mathrm{257}}−\mathrm{1}}{\mathrm{2}}}−\sqrt[{\mathrm{3}}]{\frac{\sqrt{\mathrm{257}}+\mathrm{1}}{\mathrm{2}}}}\right) \\ $$

Commented by Frix last updated on 19/Aug/23

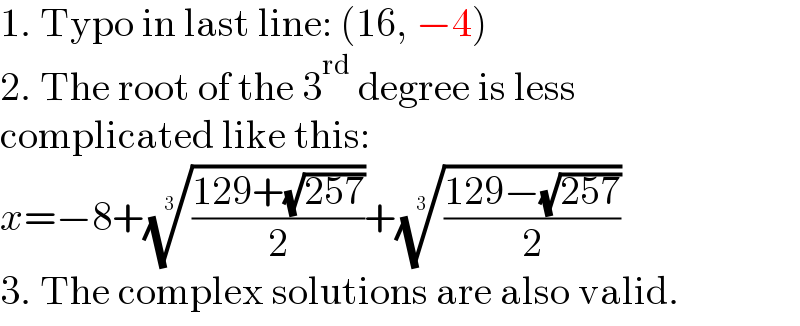
1. Typo in last line: (16, −4) 2. The root of the 3^(rd) degree is less complicated like this: x=−8+(((129+(√(257)))/2))^(1/3) +(((129−(√(257)))/2))^(1/3) 3. The complex solutions are also valid.

$$\mathrm{1}.\:\mathrm{Typo}\:\mathrm{in}\:\mathrm{last}\:\mathrm{line}:\:\left(\mathrm{16},\:−\mathrm{4}\right) \\ $$$$\mathrm{2}.\:\mathrm{The}\:\mathrm{root}\:\mathrm{of}\:\mathrm{the}\:\mathrm{3}^{\mathrm{rd}} \:\mathrm{degree}\:\mathrm{is}\:\mathrm{less} \\ $$$$\mathrm{complicated}\:\mathrm{like}\:\mathrm{this}: \\ $$$${x}=−\mathrm{8}+\sqrt[{\mathrm{3}}]{\frac{\mathrm{129}+\sqrt{\mathrm{257}}}{\mathrm{2}}}+\sqrt[{\mathrm{3}}]{\frac{\mathrm{129}−\sqrt{\mathrm{257}}}{\mathrm{2}}} \\ $$$$\mathrm{3}.\:\mathrm{The}\:\mathrm{complex}\:\mathrm{solutions}\:\mathrm{are}\:\mathrm{also}\:\mathrm{valid}. \\ $$

Commented by mathlove last updated on 20/Aug/23

thanks

$${thanks} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com