
Previous in Permutation and Combination Next in Permutation and Combination
Question Number 196143 by mr W last updated on 18/Aug/23

$${say}\:{you}\:{have}\:\mathrm{3}\:\left({different}\right)\:{books} \\ $$$${about}\:{mathematics},\:\mathrm{4}\:\left({different}\right) \\ $$$${books}\:{about}\:{physics}\:{and}\:\mathrm{5}\:\left({different}\right) \\ $$$${books}\:{about}\:{chemistry}.\:{in}\:{how}\:{many} \\ $$$${ways}\:{can}\:{you}\:{arrange}\:{them}\:{in}\:{a}\:{shelf} \\ $$$${such}\:{that}\:{no}\:{two}\:{books}\:{from}\:{the}\:{same} \\ $$$${subject}\:{are}\:{adjacent}? \\ $$
Answered by liuxinnan last updated on 19/Aug/23

Commented by mr W last updated on 19/Aug/23

$${thanks}\:{for}\:{trying}\:{sir}!\:{it}'{s}\:{not}\:{easy}\:{to} \\ $$$${follow}\:{your}\:{solution}.\:{can}\:{you}\:{please} \\ $$$${recheck}\:{your}\:{calculation}?\:{i}\:{got}\:{a} \\ $$$${slightly}\:{different}\:{result}. \\ $$
Commented by mr W last updated on 19/Aug/23
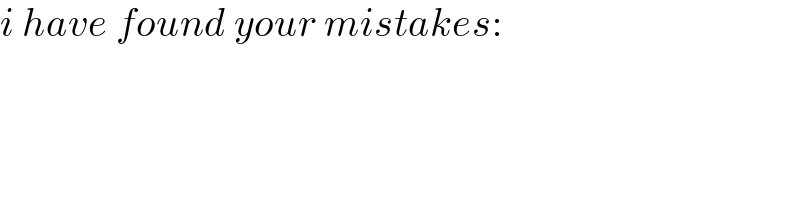
$${i}\:{have}\:{found}\:{your}\:{mistakes}: \\ $$
Commented by mr W last updated on 19/Aug/23

Commented by mr W last updated on 19/Aug/23

$${error}\:\mathrm{1}:\:{MP}\:{can}\:{also}\:{be}\:{PM}. \\ $$$${error}\:\mathrm{2}:\:{PMPM}\:{can}\:{also}\:{be}\:{MPMP}. \\ $$
Commented by liuxinnan last updated on 19/Aug/23
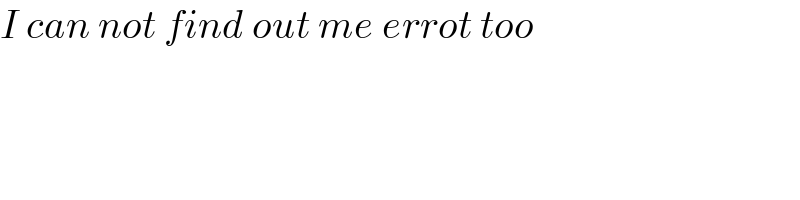
$${I}\:{can}\:{not}\:{find}\:{out}\:{me}\:{errot}\:{too} \\ $$
Commented by liuxinnan last updated on 20/Aug/23

$${thanks}\:{sir} \\ $$
Answered by mr W last updated on 19/Aug/23

$${in}\:{following}\: \\ $$$$\clubsuit\:=\:{a}\:{book}\:{for}\:{physics} \\ $$$$\blacklozenge\:=\:{a}\:{book}\:{for}\:{mathematics} \\ $$$$\bigstar=\:{a}\:{book}\:{for}\:{chemistry} \\ $$$$ \\ $$$${we}\:{arrange}\:{at}\:{first}\:{the}\:\mathrm{5}\:{books}\:{for} \\ $$$${chemistry}: \\ $$$$\Box\bigstar\boxdot\bigstar\boxdot\bigstar\boxdot\bigstar\boxdot\bigstar\Box \\ $$$$ \\ $$$${in}\:{each}\:{of}\:{the}\:\Box\:{boxes}\:{we}\:{can}\:{put} \\ $$$${nothing},\:{i}.{e}.\:{empty}\:\Leftrightarrow\mathrm{0} \\ $$$$\clubsuit\:\Leftrightarrow\mathrm{1} \\ $$$$\blacklozenge\:\:\Leftrightarrow\mathrm{100} \\ $$$$\clubsuit\blacklozenge\:\Leftrightarrow\mathrm{101}\:\:\:\left(\mathrm{2}×\right) \\ $$$$\clubsuit\blacklozenge\clubsuit\:\Leftrightarrow\mathrm{102}\: \\ $$$$\blacklozenge\clubsuit\blacklozenge\:\Leftrightarrow\mathrm{201} \\ $$$$\clubsuit\blacklozenge\clubsuit\blacklozenge\:\Leftrightarrow\mathrm{202}\:\:\:\left(\mathrm{2}×\right) \\ $$$$\clubsuit\blacklozenge\clubsuit\blacklozenge\clubsuit\:\Leftrightarrow\mathrm{203}\: \\ $$$$\blacklozenge\clubsuit\blacklozenge\clubsuit\blacklozenge\:\Leftrightarrow\mathrm{302} \\ $$$$\clubsuit\blacklozenge\clubsuit\blacklozenge\clubsuit\blacklozenge\:\Leftrightarrow\mathrm{303}\:\:\:\left(\mathrm{2}×\right) \\ $$$$\clubsuit\blacklozenge\clubsuit\blacklozenge\clubsuit\blacklozenge\clubsuit\:\Leftrightarrow\mathrm{304} \\ $$$$ \\ $$$${in}\:{each}\:{of}\:{the}\:\boxdot\:{boxes}\:{we}\:{can}\:{do}\:{as} \\ $$$${above},\:{but}\:{empty}\:{is}\:{not}\:{allowed}. \\ $$$$ \\ $$$${so}\:{we}\:{get}\:{a}\:{generating}\:{function} \\ $$$$\left(\mathrm{1}+{x}+{x}^{\mathrm{100}} +\mathrm{2}{x}^{\mathrm{101}} +{x}^{\mathrm{102}} +{x}^{\mathrm{201}} +\mathrm{2}{x}^{\mathrm{202}} +{x}^{\mathrm{203}} +{x}^{\mathrm{302}} +\mathrm{2}{x}^{\mathrm{303}} +{x}^{\mathrm{304}} \right)^{\mathrm{2}} \left({x}+{x}^{\mathrm{100}} +\mathrm{2}{x}^{\mathrm{101}} +{x}^{\mathrm{102}} +{x}^{\mathrm{201}} +\mathrm{2}{x}^{\mathrm{202}} +{x}^{\mathrm{203}} +{x}^{\mathrm{302}} +\mathrm{2}{x}^{\mathrm{303}} +{x}^{\mathrm{304}} \right)^{\mathrm{4}} \\ $$$${whose}\:{coefficient}\:{of}\:{term}\:{x}^{\mathrm{304}} \:{is}\:\mathrm{588}. \\ $$$$\Rightarrow{total}\:{number}\:{of}\:{ways}\:{is}\: \\ $$$$\:\:\:\:\mathrm{588}×\mathrm{5}!×\mathrm{4}!×\mathrm{3}!=\mathrm{10}\:\mathrm{160}\:\mathrm{640} \\ $$
Commented by mr W last updated on 19/Aug/23

