
Question Number 196134 by sonukgindia last updated on 18/Aug/23

Answered by deleteduser1 last updated on 18/Aug/23
![[log(x)+log(y)]^2 −2log(x)log(y)=2log(xy) ⇒[log(xy)]^2 =2[log(xy)+log(x)log(y)]...(i) Let [log(xy)]=t;(i)⇒t^2 −2t=2log(x)log(y) ≤[log(x)]^2 +[log(y)]^2 =2log(xy)=2q⇒t^2 ≤4t ⇒t≤4(since q>0)⇒t^2 =[log(xy)]^2 ≤16](Q196144.png)
$$\left[{log}\left({x}\right)+{log}\left({y}\right)\right]^{\mathrm{2}} −\mathrm{2}{log}\left({x}\right){log}\left({y}\right)=\mathrm{2}{log}\left({xy}\right) \\ $$$$\Rightarrow\left[{log}\left({xy}\right)\right]^{\mathrm{2}} =\mathrm{2}\left[{log}\left({xy}\right)+{log}\left({x}\right){log}\left({y}\right)\right]...\left({i}\right) \\ $$$${Let}\:\left[{log}\left({xy}\right)\right]={t};\left({i}\right)\Rightarrow{t}^{\mathrm{2}} −\mathrm{2}{t}=\mathrm{2}{log}\left({x}\right){log}\left({y}\right) \\ $$$$\leqslant\left[{log}\left({x}\right)\right]^{\mathrm{2}} +\left[{log}\left({y}\right)\right]^{\mathrm{2}} =\mathrm{2}{log}\left({xy}\right)=\mathrm{2}{q}\Rightarrow{t}^{\mathrm{2}} \leqslant\mathrm{4}{t} \\ $$$$\Rightarrow{t}\leqslant\mathrm{4}\left({since}\:{q}>\mathrm{0}\right)\Rightarrow{t}^{\mathrm{2}} =\left[{log}\left({xy}\right)\right]^{\mathrm{2}} \leqslant\mathrm{16} \\ $$
Answered by MM42 last updated on 21/Aug/23
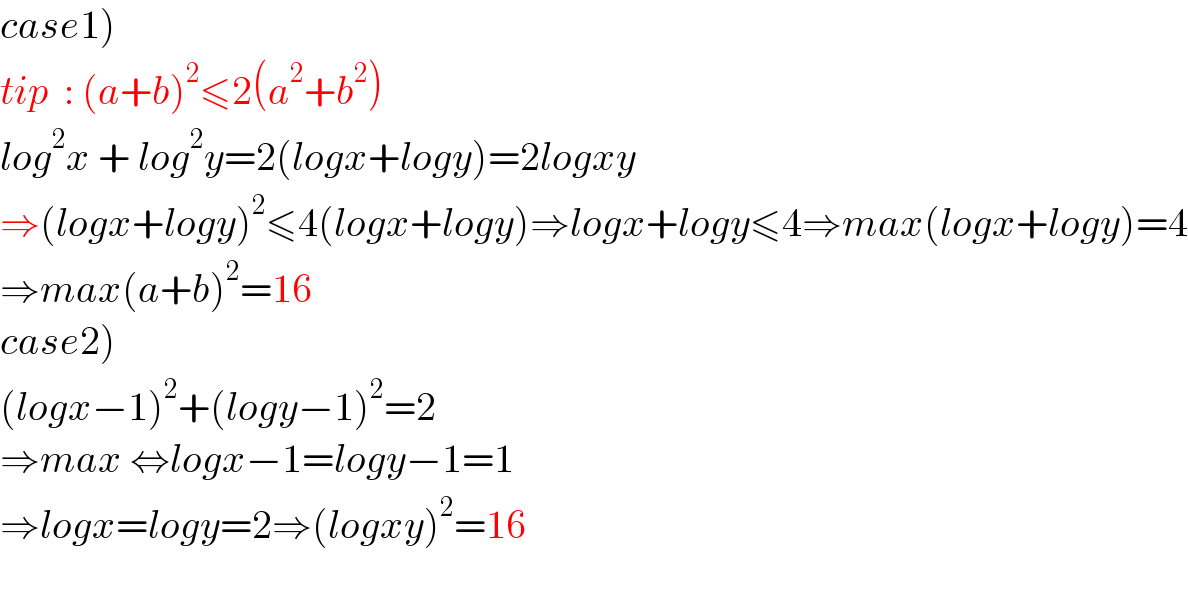
$$\left.{case}\mathrm{1}\right) \\ $$$${tip}\:\::\:\left({a}+{b}\right)^{\mathrm{2}} \leqslant\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right) \\ $$$${log}^{\mathrm{2}} {x}\:+\:{log}^{\mathrm{2}} {y}=\mathrm{2}\left({logx}+{logy}\right)=\mathrm{2}{logxy}\: \\ $$$$\Rightarrow\left({logx}+{logy}\right)^{\mathrm{2}} \leqslant\mathrm{4}\left({logx}+{logy}\right)\Rightarrow{logx}+{logy}\leqslant\mathrm{4}\Rightarrow{max}\left({logx}+{logy}\right)=\mathrm{4} \\ $$$$\Rightarrow{max}\left({a}+{b}\right)^{\mathrm{2}} =\mathrm{16} \\ $$$$\left.{case}\mathrm{2}\right) \\ $$$$\left({logx}−\mathrm{1}\right)^{\mathrm{2}} +\left({logy}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{2} \\ $$$$\Rightarrow{max}\:\Leftrightarrow{logx}−\mathrm{1}={logy}−\mathrm{1}=\mathrm{1} \\ $$$$\Rightarrow{logx}={logy}=\mathrm{2}\Rightarrow\left({logxy}\right)^{\mathrm{2}} =\mathrm{16} \\ $$$$ \\ $$
Answered by mr W last updated on 18/Aug/23
![let p=log (x), q=log (y) p^2 +q^2 =2(p+q) (p+q)^2 −2pq=2(p+q) (p+q)^2 −2(p+q)−2pq=0 ⇒p+q=1+(√(1+2pq))≤1+(√(1+(((p+q)^2 )/2))) ⇒(p+q)^2 −2(p+q)≤(((p+q)^2 )/2) ⇒(p+q)≤4 [log (xy)]^2 =(p+q)^2 ≤4^2 =16 =maximum](Q196149.png)
$${let}\:{p}=\mathrm{log}\:\left({x}\right),\:{q}=\mathrm{log}\:\left({y}\right) \\ $$$${p}^{\mathrm{2}} +{q}^{\mathrm{2}} =\mathrm{2}\left({p}+{q}\right) \\ $$$$\left({p}+{q}\right)^{\mathrm{2}} −\mathrm{2}{pq}=\mathrm{2}\left({p}+{q}\right) \\ $$$$\left({p}+{q}\right)^{\mathrm{2}} −\mathrm{2}\left({p}+{q}\right)−\mathrm{2}{pq}=\mathrm{0} \\ $$$$\Rightarrow{p}+{q}=\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{2}{pq}}\leqslant\mathrm{1}+\sqrt{\mathrm{1}+\frac{\left({p}+{q}\right)^{\mathrm{2}} }{\mathrm{2}}} \\ $$$$\Rightarrow\left({p}+{q}\right)^{\mathrm{2}} −\mathrm{2}\left({p}+{q}\right)\leqslant\frac{\left({p}+{q}\right)^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\Rightarrow\left({p}+{q}\right)\leqslant\mathrm{4} \\ $$$$\left[\mathrm{log}\:\left({xy}\right)\right]^{\mathrm{2}} =\left({p}+{q}\right)^{\mathrm{2}} \leqslant\mathrm{4}^{\mathrm{2}} =\mathrm{16}\:={maximum} \\ $$
