
Question Number 196085 by sonukgindia last updated on 17/Aug/23
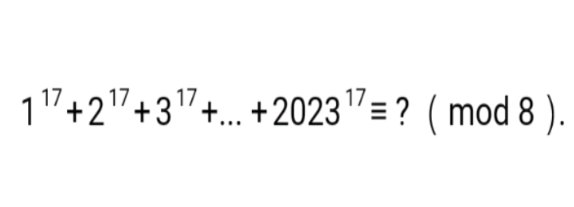
Answered by MM42 last updated on 17/Aug/23
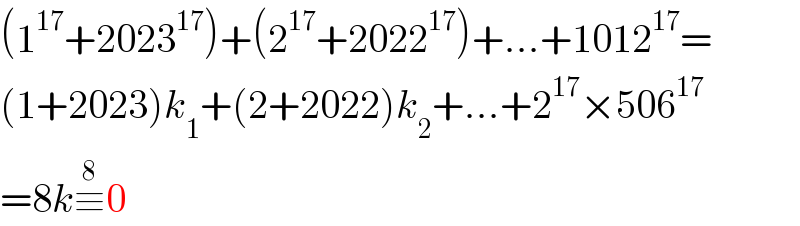
$$\left(\mathrm{1}^{\mathrm{17}} +\mathrm{2023}^{\mathrm{17}} \right)+\left(\mathrm{2}^{\mathrm{17}} +\mathrm{2022}^{\mathrm{17}} \right)+...+\mathrm{1012}^{\mathrm{17}} = \\ $$$$\left(\mathrm{1}+\mathrm{2023}\right){k}_{\mathrm{1}} +\left(\mathrm{2}+\mathrm{2022}\right){k}_{\mathrm{2}} +...+\mathrm{2}^{\mathrm{17}} ×\mathrm{506}^{\mathrm{17}} \\ $$$$=\mathrm{8}{k}\overset{\mathrm{8}} {\equiv}\mathrm{0} \\ $$
Answered by qaz last updated on 18/Aug/23
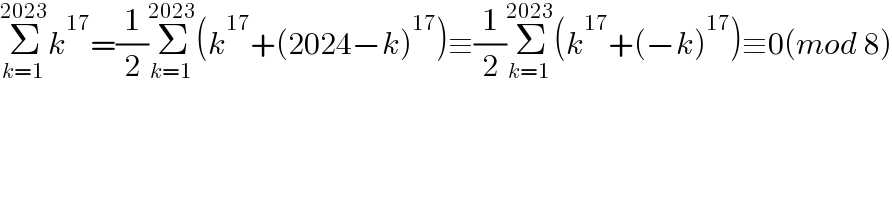
$$\underset{{k}=\mathrm{1}} {\overset{\mathrm{2023}} {\sum}}{k}^{\mathrm{17}} =\frac{\mathrm{1}}{\mathrm{2}}\underset{{k}=\mathrm{1}} {\overset{\mathrm{2023}} {\sum}}\left({k}^{\mathrm{17}} +\left(\mathrm{2024}−{k}\right)^{\mathrm{17}} \right)\equiv\frac{\mathrm{1}}{\mathrm{2}}\underset{{k}=\mathrm{1}} {\overset{\mathrm{2023}} {\sum}}\left({k}^{\mathrm{17}} +\left(−{k}\right)^{\mathrm{17}} \right)\equiv\mathrm{0}\left({mod}\:\mathrm{8}\right) \\ $$
