
Question Number 196062 by qaz last updated on 17/Aug/23
![Σ_(i=1) ^n Σ_(j=1) ^n [gcd(i,j)=1]=? ,[D]= { ((1, D is ture.)),((0, D is false. )) :}](Q196062.png)
$$\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\underset{{j}=\mathrm{1}} {\overset{{n}} {\sum}}\left[{gcd}\left({i},{j}\right)=\mathrm{1}\right]=?\:\:\:\:\:\:\:\:\:,\left[{D}\right]=\begin{cases}{\mathrm{1},\:\:\:{D}\:{is}\:{ture}.}\\{\mathrm{0},\:\:\:\:{D}\:{is}\:{false}.\:\:\:}\end{cases} \\ $$
Commented by mr W last updated on 17/Aug/23
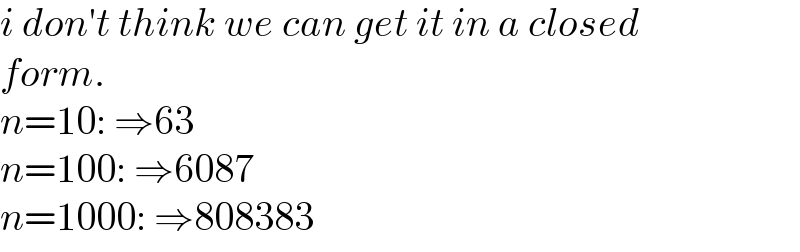
$${i}\:{don}'{t}\:{think}\:{we}\:{can}\:{get}\:{it}\:{in}\:{a}\:{closed} \\ $$$${form}. \\ $$$${n}=\mathrm{10}:\:\Rightarrow\mathrm{63} \\ $$$${n}=\mathrm{100}:\:\Rightarrow\mathrm{6087} \\ $$$${n}=\mathrm{1000}:\:\Rightarrow\mathrm{808383} \\ $$
Answered by witcher3 last updated on 17/Aug/23
![A_n =Σ_(i,j≤n) [gcd(i,j)=1] A_(n+1) =Σ_(i,j≤n+1) [gcd(i,j)=1] =A_n +2Σ_(m=1) ^(n+1) [gcd(n+1,m)] =A_n +2ϕ(n+1)..ϕ euler indecatrice function ϕ(n)=card(i,gcd(i,n)=1) ⇒A_(n+1) −A_n =2ϕ(n+1) ⇒Σ_(k=1) ^(n−1) A_(k+1) −A_k =2Σ_(k=1) ^(n−1) ϕ(k+1),n≥2 ⇒A_n −A_1 =2Σ_(k=1) ^(n−1) ϕ(k) A_n =1+2Σ_(k=1) ^(n−1) ϕ(k)](Q196082.png)
$$\mathrm{A}_{\mathrm{n}} =\underset{\mathrm{i},\mathrm{j}\leqslant\mathrm{n}} {\sum}\left[\mathrm{gcd}\left(\mathrm{i},\mathrm{j}\right)=\mathrm{1}\right] \\ $$$$\mathrm{A}_{\mathrm{n}+\mathrm{1}} =\underset{\mathrm{i},\mathrm{j}\leqslant\mathrm{n}+\mathrm{1}} {\sum}\left[\mathrm{gcd}\left(\mathrm{i},\mathrm{j}\right)=\mathrm{1}\right] \\ $$$$=\mathrm{A}_{\mathrm{n}} +\mathrm{2}\underset{\mathrm{m}=\mathrm{1}} {\overset{\mathrm{n}+\mathrm{1}} {\sum}}\left[\mathrm{gcd}\left(\mathrm{n}+\mathrm{1},\mathrm{m}\right)\right] \\ $$$$=\mathrm{A}_{\mathrm{n}} +\mathrm{2}\varphi\left(\mathrm{n}+\mathrm{1}\right)..\varphi\:\mathrm{euler}\:\mathrm{indecatrice}\:\mathrm{function} \\ $$$$\varphi\left(\mathrm{n}\right)=\mathrm{card}\left(\mathrm{i},\mathrm{gcd}\left(\mathrm{i},\mathrm{n}\right)=\mathrm{1}\right) \\ $$$$\Rightarrow\mathrm{A}_{\mathrm{n}+\mathrm{1}} −\mathrm{A}_{\mathrm{n}} =\mathrm{2}\varphi\left(\mathrm{n}+\mathrm{1}\right) \\ $$$$\Rightarrow\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}−\mathrm{1}} {\sum}}\mathrm{A}_{\mathrm{k}+\mathrm{1}} −\mathrm{A}_{\mathrm{k}} =\mathrm{2}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}−\mathrm{1}} {\sum}}\varphi\left(\mathrm{k}+\mathrm{1}\right),\mathrm{n}\geqslant\mathrm{2} \\ $$$$\Rightarrow\mathrm{A}_{\mathrm{n}} −\mathrm{A}_{\mathrm{1}} =\mathrm{2}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}−\mathrm{1}} {\sum}}\varphi\left(\mathrm{k}\right) \\ $$$$\mathrm{A}_{\mathrm{n}} =\mathrm{1}+\mathrm{2}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}−\mathrm{1}} {\sum}}\varphi\left(\mathrm{k}\right) \\ $$
