
Question Number 196056 by mr W last updated on 17/Aug/23
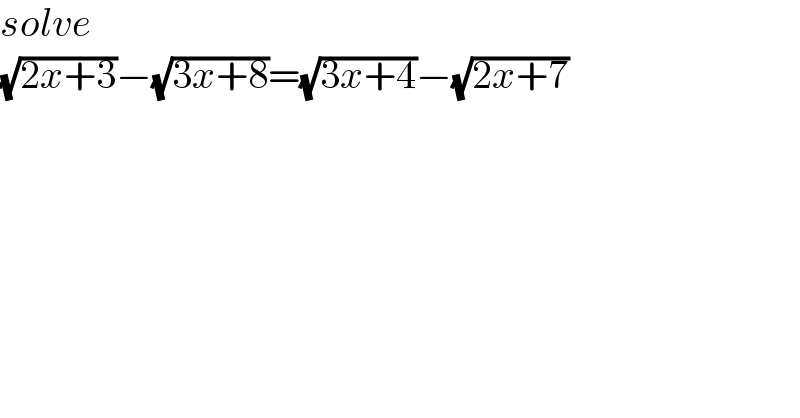
$${solve} \\ $$$$\sqrt{\mathrm{2}{x}+\mathrm{3}}−\sqrt{\mathrm{3}{x}+\mathrm{8}}=\sqrt{\mathrm{3}{x}+\mathrm{4}}−\sqrt{\mathrm{2}{x}+\mathrm{7}} \\ $$
Answered by cortano12 last updated on 17/Aug/23
![(√u) −(√(v+4)) =(√v)−(√(u+4)) (√u)−(√v) = (√(v+4))−(√(u+4)) u+v−2(√(uv)) = u+v+8−2(√((u+4)(v+4))) (√((u+4)(v+4))) = 4+(√(uv)) uv+4(u+v)+16=16+uv+8(√(uv)) u+v = 2(√(uv)) ((√u)−(√v) )= 0 (√u) = (√v) ; [ { ((u=2x+3)),((v=3x+4)) :} ] ⇔ 3x+4 = 2x+3 ⇔ x=−1](Q196057.png)
$$\:\sqrt{\mathrm{u}}\:−\sqrt{\mathrm{v}+\mathrm{4}}\:=\sqrt{\mathrm{v}}−\sqrt{\mathrm{u}+\mathrm{4}} \\ $$$$\:\:\sqrt{\mathrm{u}}−\sqrt{\mathrm{v}}\:=\:\sqrt{\mathrm{v}+\mathrm{4}}−\sqrt{\mathrm{u}+\mathrm{4}} \\ $$$$\:\:\mathrm{u}+\mathrm{v}−\mathrm{2}\sqrt{\mathrm{uv}}\:=\:\mathrm{u}+\mathrm{v}+\mathrm{8}−\mathrm{2}\sqrt{\left(\mathrm{u}+\mathrm{4}\right)\left(\mathrm{v}+\mathrm{4}\right)} \\ $$$$\:\:\sqrt{\left(\mathrm{u}+\mathrm{4}\right)\left(\mathrm{v}+\mathrm{4}\right)}\:=\:\mathrm{4}+\sqrt{\mathrm{uv}} \\ $$$$\:\:\mathrm{uv}+\mathrm{4}\left(\mathrm{u}+\mathrm{v}\right)+\mathrm{16}=\mathrm{16}+\mathrm{uv}+\mathrm{8}\sqrt{\mathrm{uv}} \\ $$$$\:\:\:\mathrm{u}+\mathrm{v}\:=\:\mathrm{2}\sqrt{\mathrm{uv}} \\ $$$$\:\:\:\left(\sqrt{\mathrm{u}}−\sqrt{\mathrm{v}}\:\right)=\:\mathrm{0} \\ $$$$\:\:\:\sqrt{\mathrm{u}}\:=\:\sqrt{\mathrm{v}}\:;\:\left[\:\begin{cases}{\mathrm{u}=\mathrm{2x}+\mathrm{3}}\\{\mathrm{v}=\mathrm{3x}+\mathrm{4}}\end{cases}\:\right]\: \\ $$$$\:\:\Leftrightarrow\:\mathrm{3x}+\mathrm{4}\:=\:\mathrm{2x}+\mathrm{3} \\ $$$$\:\:\Leftrightarrow\:\mathrm{x}=−\mathrm{1}\: \\ $$
Commented by mr W last updated on 17/Aug/23

$${very}\:{nice}! \\ $$
Answered by mr W last updated on 17/Aug/23
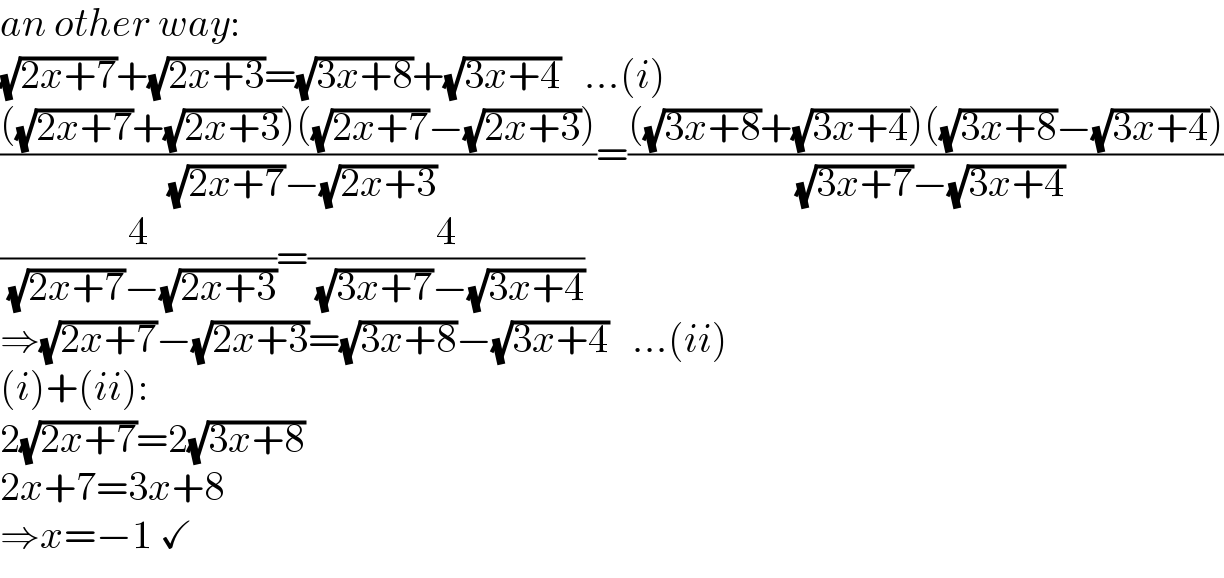
$${an}\:{other}\:{way}: \\ $$$$\sqrt{\mathrm{2}{x}+\mathrm{7}}+\sqrt{\mathrm{2}{x}+\mathrm{3}}=\sqrt{\mathrm{3}{x}+\mathrm{8}}+\sqrt{\mathrm{3}{x}+\mathrm{4}}\:\:\:...\left({i}\right) \\ $$$$\frac{\left(\sqrt{\mathrm{2}{x}+\mathrm{7}}+\sqrt{\mathrm{2}{x}+\mathrm{3}}\right)\left(\sqrt{\mathrm{2}{x}+\mathrm{7}}−\sqrt{\mathrm{2}{x}+\mathrm{3}}\right)}{\:\sqrt{\mathrm{2}{x}+\mathrm{7}}−\sqrt{\mathrm{2}{x}+\mathrm{3}}}=\frac{\left(\sqrt{\mathrm{3}{x}+\mathrm{8}}+\sqrt{\mathrm{3}{x}+\mathrm{4}}\right)\left(\sqrt{\mathrm{3}{x}+\mathrm{8}}−\sqrt{\mathrm{3}{x}+\mathrm{4}}\right)}{\:\sqrt{\mathrm{3}{x}+\mathrm{7}}−\sqrt{\mathrm{3}{x}+\mathrm{4}}} \\ $$$$\frac{\mathrm{4}}{\:\sqrt{\mathrm{2}{x}+\mathrm{7}}−\sqrt{\mathrm{2}{x}+\mathrm{3}}}=\frac{\mathrm{4}}{\:\sqrt{\mathrm{3}{x}+\mathrm{7}}−\sqrt{\mathrm{3}{x}+\mathrm{4}}} \\ $$$$\Rightarrow\sqrt{\mathrm{2}{x}+\mathrm{7}}−\sqrt{\mathrm{2}{x}+\mathrm{3}}=\sqrt{\mathrm{3}{x}+\mathrm{8}}−\sqrt{\mathrm{3}{x}+\mathrm{4}}\:\:\:...\left({ii}\right) \\ $$$$\left({i}\right)+\left({ii}\right): \\ $$$$\mathrm{2}\sqrt{\mathrm{2}{x}+\mathrm{7}}=\mathrm{2}\sqrt{\mathrm{3}{x}+\mathrm{8}} \\ $$$$\mathrm{2}{x}+\mathrm{7}=\mathrm{3}{x}+\mathrm{8} \\ $$$$\Rightarrow{x}=−\mathrm{1}\:\checkmark \\ $$
Commented by MM42 last updated on 17/Aug/23
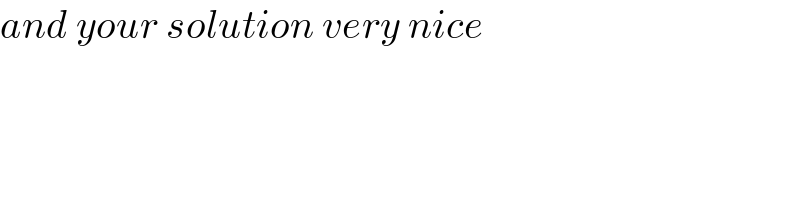
$${and}\:{your}\:{solution}\:{very}\:{nice} \\ $$
Answered by MM42 last updated on 17/Aug/23
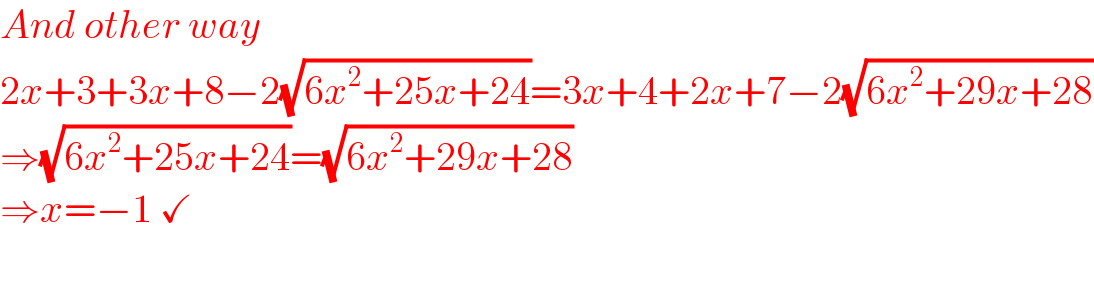
$${And}\:{other}\:{way} \\ $$$$\mathrm{2}{x}+\mathrm{3}+\mathrm{3}{x}+\mathrm{8}−\mathrm{2}\sqrt{\mathrm{6}{x}^{\mathrm{2}} +\mathrm{25}{x}+\mathrm{24}}=\mathrm{3}{x}+\mathrm{4}+\mathrm{2}{x}+\mathrm{7}−\mathrm{2}\sqrt{\mathrm{6}{x}^{\mathrm{2}} +\mathrm{29}{x}+\mathrm{28}} \\ $$$$\Rightarrow\sqrt{\mathrm{6}{x}^{\mathrm{2}} +\mathrm{25}{x}+\mathrm{24}}=\sqrt{\mathrm{6}{x}^{\mathrm{2}} +\mathrm{29}{x}+\mathrm{28}} \\ $$$$\Rightarrow{x}=−\mathrm{1}\:\checkmark \\ $$$$ \\ $$
Answered by Rasheed.Sindhi last updated on 17/Aug/23

$$\underset{−} {\sqrt{\mathrm{2}{x}+\mathrm{3}}−\sqrt{\mathrm{3}{x}+\mathrm{8}}=\sqrt{\mathrm{3}{x}+\mathrm{4}}−\sqrt{\mathrm{2}{x}+\mathrm{7}}\:} \\ $$$$\sqrt{\mathrm{2}{x}+\mathrm{5}−\mathrm{2}}\:+\sqrt{\mathrm{2}{x}+\mathrm{5}+\mathrm{2}}\:=\sqrt{\mathrm{3}{x}+\mathrm{6}−\mathrm{2}}\:+\sqrt{\mathrm{3}{x}+\mathrm{6}+\mathrm{2}}\: \\ $$$$\:\:\:\:\mathrm{2}{x}+\mathrm{5}={a}\:\:,\:\mathrm{3}{x}+\mathrm{6}={b} \\ $$$$\sqrt{{a}−\mathrm{2}}\:+\sqrt{{a}+\mathrm{2}}\:=\sqrt{{b}−\mathrm{2}}\:+\sqrt{{b}+\mathrm{2}}\:={c}\:\left({say}\right) \\ $$$$ \\ $$$$\:\:\sqrt{{a}−\mathrm{2}}\:+\sqrt{{a}+\mathrm{2}}\:={c}.........\left({i}\right) \\ $$$$\:\:\left(\sqrt{{a}−\mathrm{2}}\:\right)^{\mathrm{2}} −\left(\sqrt{{a}+\mathrm{2}}\:\right)^{\mathrm{2}} \:=\left({a}−\mathrm{2}\right)−\left({a}+\mathrm{2}\right)=−\mathrm{4}...\left({ii}\right) \\ $$$$\left({ii}\right)/\left({i}\right): \\ $$$$\:\:\:\sqrt{{a}−\mathrm{2}}\:−\sqrt{{a}+\mathrm{2}}\:=\frac{−\mathrm{4}}{{c}}.......\left({iii}\right) \\ $$$$\left({i}\right)+\left({iii}\right): \\ $$$$\:\:\:\mathrm{2}\sqrt{{a}−\mathrm{2}}\:={c}−\frac{\mathrm{4}}{{c}}.....\left({iv}\right) \\ $$$${Similarly}, \\ $$$$\:\:\:\:\mathrm{2}\sqrt{{b}−\mathrm{2}}\:={c}−\frac{\mathrm{4}}{{c}}.....\left({v}\right) \\ $$$$\left({iv}\right)\:\&\:\left({v}\right):\:\mathrm{2}\sqrt{{a}−\mathrm{2}}\:=\mathrm{2}\sqrt{{b}−\mathrm{2}}\: \\ $$$${a}={b}\Rightarrow\mathrm{2}{x}+\mathrm{5}=\mathrm{3}{x}+\mathrm{6} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}=−\mathrm{1} \\ $$
Answered by Frix last updated on 17/Aug/23
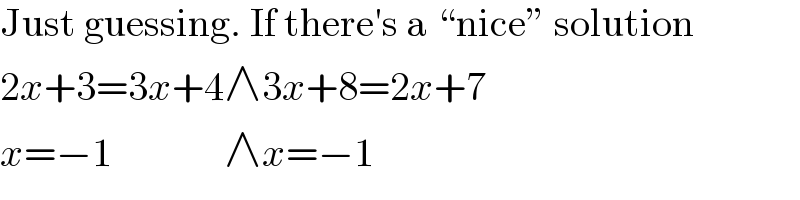
$$\mathrm{Just}\:\mathrm{guessing}.\:\mathrm{If}\:\mathrm{there}'\mathrm{s}\:\mathrm{a}\:``\mathrm{nice}''\:\mathrm{solution} \\ $$$$\mathrm{2}{x}+\mathrm{3}=\mathrm{3}{x}+\mathrm{4}\wedge\mathrm{3}{x}+\mathrm{8}=\mathrm{2}{x}+\mathrm{7} \\ $$$${x}=−\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\wedge{x}=−\mathrm{1} \\ $$
