Question and Answers Forum

All Questions      Topic List

Number Theory Questions

Previous in All Question      Next in All Question      

Previous in Number Theory      Next in Number Theory      

Question Number 196053 by mathlove last updated on 17/Aug/23

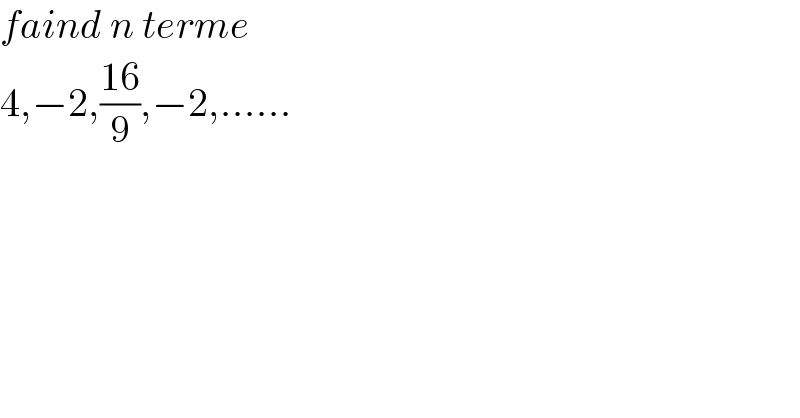
faind n terme 4,−2,((16)/9),−2,......

$${faind}\:{n}\:{terme} \\ $$$$\mathrm{4},−\mathrm{2},\frac{\mathrm{16}}{\mathrm{9}},−\mathrm{2},...... \\ $$

Answered by Frix last updated on 17/Aug/23

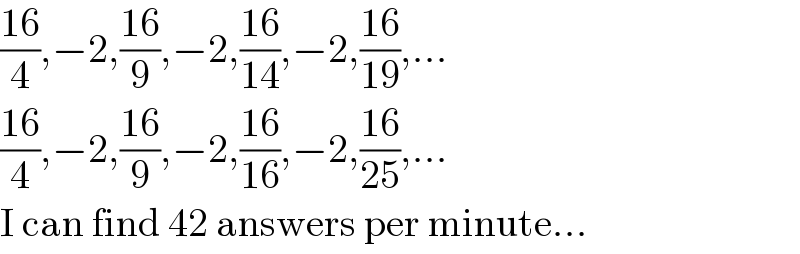
((16)/4),−2,((16)/9),−2,((16)/(14)),−2,((16)/(19)),... ((16)/4),−2,((16)/9),−2,((16)/(16)),−2,((16)/(25)),... I can find 42 answers per minute...

$$\frac{\mathrm{16}}{\mathrm{4}},−\mathrm{2},\frac{\mathrm{16}}{\mathrm{9}},−\mathrm{2},\frac{\mathrm{16}}{\mathrm{14}},−\mathrm{2},\frac{\mathrm{16}}{\mathrm{19}},... \\ $$$$\frac{\mathrm{16}}{\mathrm{4}},−\mathrm{2},\frac{\mathrm{16}}{\mathrm{9}},−\mathrm{2},\frac{\mathrm{16}}{\mathrm{16}},−\mathrm{2},\frac{\mathrm{16}}{\mathrm{25}},... \\ $$$$\mathrm{I}\:\mathrm{can}\:\mathrm{find}\:\mathrm{42}\:\mathrm{answers}\:\mathrm{per}\:\mathrm{minute}... \\ $$

Commented by mathlove last updated on 17/Aug/23

solve it n term

$${solve}\:{it}\:{n}\:{term} \\ $$

Commented by Frix last updated on 18/Aug/23

2 possible solutions out of (1zillion)^(1zillion) a_n =−(2/9)(13n^3 −100n^2 +236n−167) b_n =−((32n^3 )/(479n^3 −3249n^2 +6530n−3768))

$$\mathrm{2}\:\mathrm{possible}\:\mathrm{solutions}\:\mathrm{out}\:\mathrm{of}\:\left(\mathrm{1zillion}\right)^{\mathrm{1zillion}} \\ $$$${a}_{{n}} =−\frac{\mathrm{2}}{\mathrm{9}}\left(\mathrm{13}{n}^{\mathrm{3}} −\mathrm{100}{n}^{\mathrm{2}} +\mathrm{236}{n}−\mathrm{167}\right) \\ $$$${b}_{{n}} =−\frac{\mathrm{32}{n}^{\mathrm{3}} }{\mathrm{479}{n}^{\mathrm{3}} −\mathrm{3249}{n}^{\mathrm{2}} +\mathrm{6530}{n}−\mathrm{3768}} \\ $$

Commented by Frix last updated on 18/Aug/23

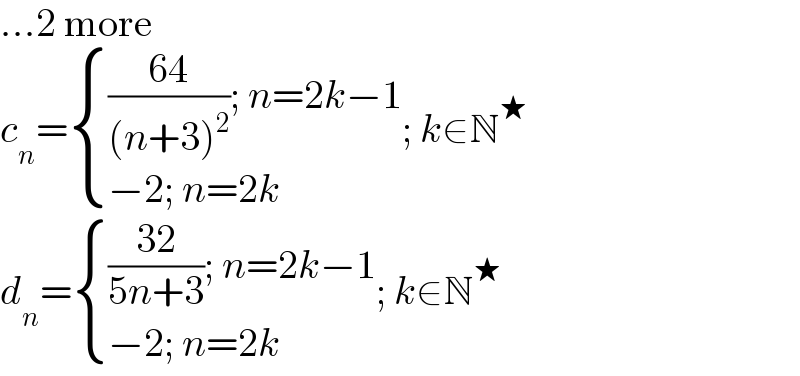
...2 more c_n = { ((((64)/((n+3)^2 )); n=2k−1)),((−2; n=2k)) :}; k∈N^★ d_n = { ((((32)/(5n+3)); n=2k−1)),((−2; n=2k)) :}; k∈N^★

$$...\mathrm{2}\:\mathrm{more} \\ $$$${c}_{{n}} =\begin{cases}{\frac{\mathrm{64}}{\left({n}+\mathrm{3}\right)^{\mathrm{2}} };\:{n}=\mathrm{2}{k}−\mathrm{1}}\\{−\mathrm{2};\:{n}=\mathrm{2}{k}}\end{cases};\:{k}\in\mathbb{N}^{\bigstar} \\ $$$${d}_{{n}} =\begin{cases}{\frac{\mathrm{32}}{\mathrm{5}{n}+\mathrm{3}};\:{n}=\mathrm{2}{k}−\mathrm{1}}\\{−\mathrm{2};\:{n}=\mathrm{2}{k}}\end{cases};\:{k}\in\mathbb{N}^{\bigstar} \\ $$

Commented by Frix last updated on 18/Aug/23

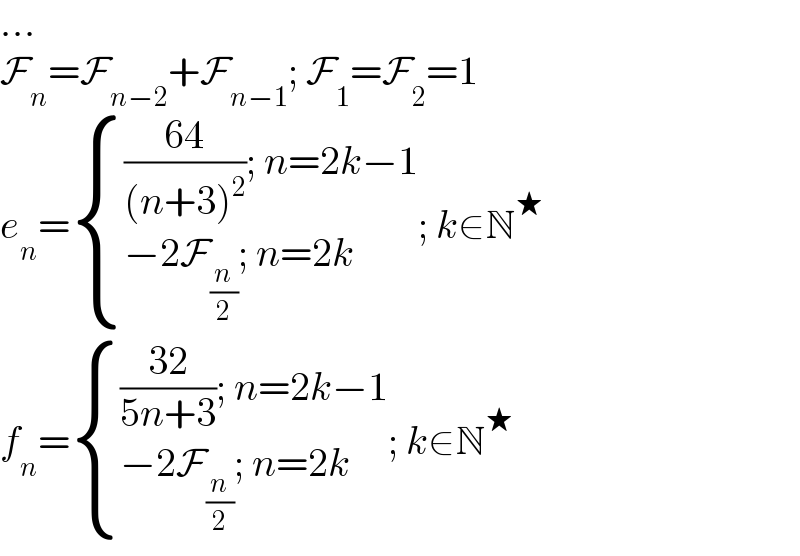
... F_n =F_(n−2) +F_(n−1) ; F_1 =F_2 =1 e_n = { ((((64)/((n+3)^2 )); n=2k−1)),((−2F_(n/2) ; n=2k)) :}; k∈N^★ f_n = { ((((32)/(5n+3)); n=2k−1)),((−2F_(n/2) ; n=2k)) :}; k∈N^★

$$... \\ $$$$\mathcal{F}_{{n}} =\mathcal{F}_{{n}−\mathrm{2}} +\mathcal{F}_{{n}−\mathrm{1}} ;\:\mathcal{F}_{\mathrm{1}} =\mathcal{F}_{\mathrm{2}} =\mathrm{1} \\ $$$${e}_{{n}} =\begin{cases}{\frac{\mathrm{64}}{\left({n}+\mathrm{3}\right)^{\mathrm{2}} };\:{n}=\mathrm{2}{k}−\mathrm{1}}\\{−\mathrm{2}\mathcal{F}_{\frac{{n}}{\mathrm{2}}} ;\:{n}=\mathrm{2}{k}}\end{cases};\:{k}\in\mathbb{N}^{\bigstar} \\ $$$${f}_{{n}} =\begin{cases}{\frac{\mathrm{32}}{\mathrm{5}{n}+\mathrm{3}};\:{n}=\mathrm{2}{k}−\mathrm{1}}\\{−\mathrm{2}\mathcal{F}_{\frac{{n}}{\mathrm{2}}} ;\:{n}=\mathrm{2}{k}}\end{cases};\:{k}\in\mathbb{N}^{\bigstar} \\ $$

Commented by mathlove last updated on 18/Aug/23

thanks

$${thanks} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com