Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 195982 by mathlove last updated on 14/Aug/23

lim_(x→1) [(1/(2(1−(√x))))−(1/(3(1−(x)^(1/3) )))]=? with out l′pital rule

$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\left[\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}−\sqrt{{x}}\right)}−\frac{\mathrm{1}}{\mathrm{3}\left(\mathrm{1}−\sqrt[{\mathrm{3}}]{{x}}\right)}\right]=? \\ $$$${with}\:{out}\:{l}'{pital}\:{rule} \\ $$

Answered by MM42 last updated on 14/Aug/23

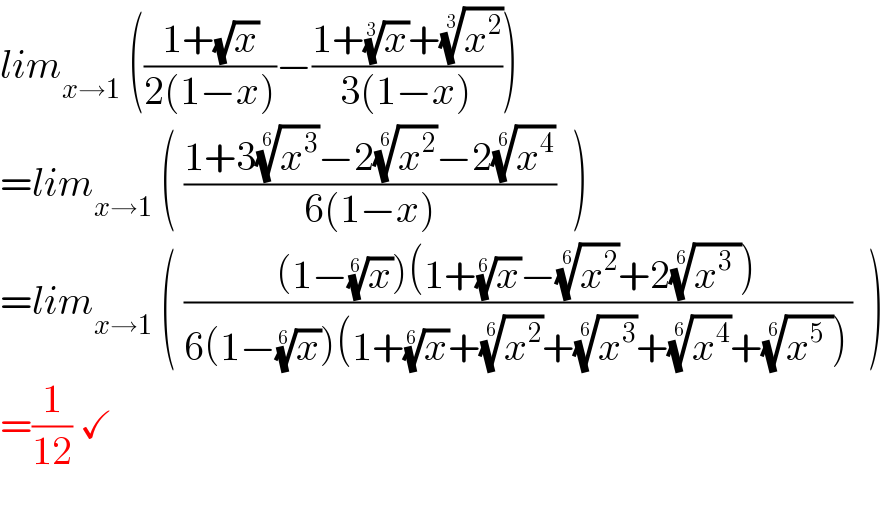
lim_(x→1) (((1+(√x))/(2(1−x)))−((1+(x)^(1/3) +(x^2 )^(1/3) )/(3(1−x)))) =lim_(x→1) ( ((1+3(x^3 )^(1/6) −2(x^2 )^(1/6) −2(x^4 )^(1/6) )/(6(1−x))) ) =lim_(x→1) ( (((1−(x)^(1/6) )(1+(x)^(1/6) −(x^2 )^(1/6) +2((x^3 ))^(1/6) ))/(6(1−(x)^(1/6) )(1+(x)^(1/6) +(x^2 )^(1/6) +(x^3 )^(1/6) +(x^4 )^(1/6) +((x^5 ))^(1/6) ))) ) =(1/(12)) ✓

$${lim}_{{x}\rightarrow\mathrm{1}} \:\left(\frac{\mathrm{1}+\sqrt{{x}}}{\mathrm{2}\left(\mathrm{1}−{x}\right)}−\frac{\mathrm{1}+\sqrt[{\mathrm{3}}]{{x}}+\sqrt[{\mathrm{3}}]{{x}^{\mathrm{2}} }}{\mathrm{3}\left(\mathrm{1}−{x}\right)}\right) \\ $$$$={lim}_{{x}\rightarrow\mathrm{1}} \:\left(\:\frac{\mathrm{1}+\mathrm{3}\sqrt[{\mathrm{6}}]{{x}^{\mathrm{3}} }−\mathrm{2}\sqrt[{\mathrm{6}}]{{x}^{\mathrm{2}} }−\mathrm{2}\sqrt[{\mathrm{6}}]{{x}^{\mathrm{4}} }}{\mathrm{6}\left(\mathrm{1}−{x}\right)}\:\:\right) \\ $$$$={lim}_{{x}\rightarrow\mathrm{1}} \:\left(\:\frac{\left(\mathrm{1}−\sqrt[{\mathrm{6}}]{{x}}\right)\left(\mathrm{1}+\sqrt[{\mathrm{6}}]{{x}}−\sqrt[{\mathrm{6}}]{{x}^{\mathrm{2}} }+\mathrm{2}\sqrt[{\mathrm{6}}]{{x}^{\mathrm{3}} \:}\right)}{\mathrm{6}\left(\mathrm{1}−\sqrt[{\mathrm{6}}]{{x}}\right)\left(\mathrm{1}+\sqrt[{\mathrm{6}}]{{x}}+\sqrt[{\mathrm{6}}]{{x}^{\mathrm{2}} }+\sqrt[{\mathrm{6}}]{{x}^{\mathrm{3}} }+\sqrt[{\mathrm{6}}]{{x}^{\mathrm{4}} }+\sqrt[{\mathrm{6}}]{{x}^{\mathrm{5}} \:}\right)}\:\:\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{12}}\:\checkmark \\ $$$$ \\ $$

Commented by mathlove last updated on 15/Aug/23

thanks

$${thanks} \\ $$

Answered by mr W last updated on 14/Aug/23

let t=(x)^(1/6) L=lim_(t→1) [(1/(2(1−t^3 )))−(1/(3(1−t^2 )))] =lim_(t→1) [((1+t^3 )/(2(1−t^6 )))−((1+t^2 +t^4 )/(3(1−t^6 )))] =lim_(t→1) [((1+2t^3 −2t^2 −2t^4 )/(6(1−t^6 )))] =lim_(t→1) [((1−t^3 −2t^2 +4t^3 −2t^4 )/(6(1−t^6 )))] =lim_(t→1) [((1−t^3 −2t^2 (1−t)^2 )/(6(1−t^6 )))] =lim_(t→1) [(1/(6(1+t^3 )))−((t^2 (1−t)^2 )/(3(1+t^3 )(1−t^3 )))] =lim_(t→1) [(1/(6(1+t^3 )))−((t^2 (1−t))/(3(1+t^3 )(1+t+t^2 )))] =(1/(6(1+1)))−((1×(1−1))/(3(1+1)(1+1+1))) =(1/(12))

$${let}\:{t}=\sqrt[{\mathrm{6}}]{{x}} \\ $$$${L}=\underset{{t}\rightarrow\mathrm{1}} {\mathrm{lim}}\left[\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}−{t}^{\mathrm{3}} \right)}−\frac{\mathrm{1}}{\mathrm{3}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)}\right] \\ $$$$\:=\underset{{t}\rightarrow\mathrm{1}} {\mathrm{lim}}\left[\frac{\mathrm{1}+{t}^{\mathrm{3}} }{\mathrm{2}\left(\mathrm{1}−{t}^{\mathrm{6}} \right)}−\frac{\mathrm{1}+{t}^{\mathrm{2}} +{t}^{\mathrm{4}} }{\mathrm{3}\left(\mathrm{1}−{t}^{\mathrm{6}} \right)}\right] \\ $$$$\:=\underset{{t}\rightarrow\mathrm{1}} {\mathrm{lim}}\left[\frac{\mathrm{1}+\mathrm{2}{t}^{\mathrm{3}} −\mathrm{2}{t}^{\mathrm{2}} −\mathrm{2}{t}^{\mathrm{4}} }{\mathrm{6}\left(\mathrm{1}−{t}^{\mathrm{6}} \right)}\right] \\ $$$$\:=\underset{{t}\rightarrow\mathrm{1}} {\mathrm{lim}}\left[\frac{\mathrm{1}−{t}^{\mathrm{3}} −\mathrm{2}{t}^{\mathrm{2}} +\mathrm{4}{t}^{\mathrm{3}} −\mathrm{2}{t}^{\mathrm{4}} }{\mathrm{6}\left(\mathrm{1}−{t}^{\mathrm{6}} \right)}\right] \\ $$$$\:=\underset{{t}\rightarrow\mathrm{1}} {\mathrm{lim}}\left[\frac{\mathrm{1}−{t}^{\mathrm{3}} −\mathrm{2}{t}^{\mathrm{2}} \left(\mathrm{1}−{t}\right)^{\mathrm{2}} }{\mathrm{6}\left(\mathrm{1}−{t}^{\mathrm{6}} \right)}\right] \\ $$$$\:=\underset{{t}\rightarrow\mathrm{1}} {\mathrm{lim}}\left[\frac{\mathrm{1}}{\mathrm{6}\left(\mathrm{1}+{t}^{\mathrm{3}} \right)}−\frac{{t}^{\mathrm{2}} \left(\mathrm{1}−{t}\right)^{\mathrm{2}} }{\mathrm{3}\left(\mathrm{1}+{t}^{\mathrm{3}} \right)\left(\mathrm{1}−{t}^{\mathrm{3}} \right)}\right] \\ $$$$\:=\underset{{t}\rightarrow\mathrm{1}} {\mathrm{lim}}\left[\frac{\mathrm{1}}{\mathrm{6}\left(\mathrm{1}+{t}^{\mathrm{3}} \right)}−\frac{{t}^{\mathrm{2}} \left(\mathrm{1}−{t}\right)}{\mathrm{3}\left(\mathrm{1}+{t}^{\mathrm{3}} \right)\left(\mathrm{1}+{t}+{t}^{\mathrm{2}} \right)}\right] \\ $$$$\:=\frac{\mathrm{1}}{\mathrm{6}\left(\mathrm{1}+\mathrm{1}\right)}−\frac{\mathrm{1}×\left(\mathrm{1}−\mathrm{1}\right)}{\mathrm{3}\left(\mathrm{1}+\mathrm{1}\right)\left(\mathrm{1}+\mathrm{1}+\mathrm{1}\right)} \\ $$$$\:=\frac{\mathrm{1}}{\mathrm{12}} \\ $$

Commented by AROUNAMoussa last updated on 14/Aug/23

cool!

$$\boldsymbol{{cool}}! \\ $$

Commented by mathlove last updated on 15/Aug/23

thanks

$${thanks} \\ $$

Terms of Service

Privacy Policy

Contact: [email protected]