
Question Number 195820 by York12 last updated on 11/Aug/23
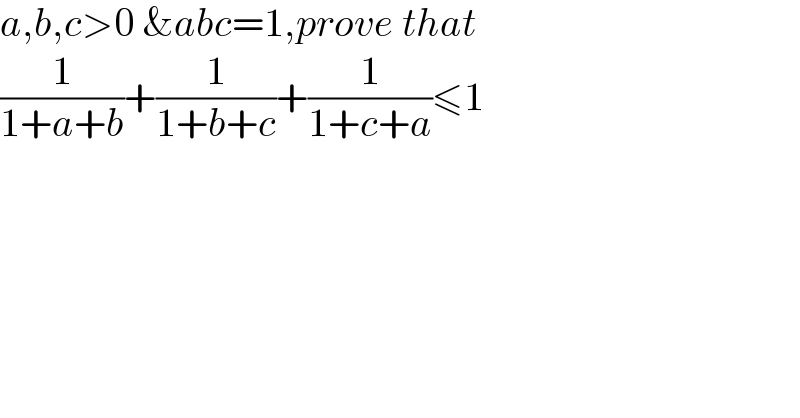
$${a},{b},{c}>\mathrm{0}\:\&{abc}=\mathrm{1},{prove}\:{that} \\ $$$$\frac{\mathrm{1}}{\mathrm{1}+{a}+{b}}+\frac{\mathrm{1}}{\mathrm{1}+{b}+{c}}+\frac{\mathrm{1}}{\mathrm{1}+{c}+{a}}\leqslant\mathrm{1} \\ $$
Answered by CrispyXYZ last updated on 12/Aug/23

$$\mathrm{let}\:{a}={x}^{\mathrm{3}} ,\:{b}={y}^{\mathrm{3}} ,\:{c}={z}^{\mathrm{3}} ,\:\mathrm{then}\:{xyz}=\mathrm{1}. \\ $$$${x}^{\mathrm{3}} +{y}^{\mathrm{3}} −{x}^{\mathrm{2}} {y}−{y}^{\mathrm{2}} {x}=\left({x}−{y}\right)^{\mathrm{2}} \left({x}+{y}\right)\geqslant\mathrm{0} \\ $$$$\Rightarrow{x}^{\mathrm{3}} +{y}^{\mathrm{3}} \geqslant{x}^{\mathrm{2}} {y}+{y}^{\mathrm{2}} {x} \\ $$$$\frac{\mathrm{1}}{\mathrm{1}+{a}+{b}}=\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{3}} +{y}^{\mathrm{3}} } \\ $$$$\leqslant\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} {y}+{y}^{\mathrm{2}} {x}} \\ $$$$=\frac{\mathrm{1}}{{xyz}+{x}^{\mathrm{2}} {y}+{y}^{\mathrm{2}} {x}}=\frac{\mathrm{1}}{{xy}\left({x}+{y}+{z}\right)}=\frac{{z}}{{x}+{y}+{z}} \\ $$$$\mathrm{Similarly}, \\ $$$$\frac{\mathrm{1}}{\mathrm{1}+{b}+{c}}\leqslant\frac{{x}}{{x}+{y}+{z}},\:\:\frac{\mathrm{1}}{\mathrm{1}+{c}+{a}}\leqslant\frac{{y}}{{x}+{y}+{z}}. \\ $$$$\mathrm{In}\:\mathrm{conclusion}, \\ $$$$\frac{\mathrm{1}}{\mathrm{1}+{a}+{b}}+\frac{\mathrm{1}}{\mathrm{1}+{b}+{c}}+\frac{\mathrm{1}}{\mathrm{1}+{a}+{c}}\leqslant\frac{{x}+{y}+{z}}{{x}+{y}+{z}}=\mathrm{1} \\ $$
Commented by York12 last updated on 13/Aug/23

$${tbanks} \\ $$
