
Previous in Permutation and Combination Next in Permutation and Combination
Question Number 195666 by uchihayahia last updated on 07/Aug/23

$$ \\ $$$$\:{sequence}\:{of}\:{string}\:{said}\:{to}\:{be}\:{orderly} \\ $$$$\:{if}\:{element}\:{index}\:{i}\:{different}\:{to}\:{i}+\mathrm{1} \\ $$$$\:{for}\:{example} \\ $$$$\:{aba}\:{has}\:{orderly}\:{value}\:\mathrm{2} \\ $$$$\:{abab}\:{has}\:{orderly}\:{value}\:\mathrm{3} \\ $$$$\:{abaabb}\:{has}\:{orderly}\:{value}\:\mathrm{3} \\ $$$$\:{if}\:{there}\:{are}\:\mathrm{7}\:{a}\:{and}\:\mathrm{13}\:{b} \\ $$$$\:{example} \\ $$$$\:{aaaaaaabbbbbbbbbbbbb}\:{has}\:{orderly}\:{value}\:\mathrm{1} \\ $$$$\:{what}\:{is}\:{the}\:{mean}\:{of}\:{its}\:{orderly}\:{value} \\ $$$$\:{for}\:{all}\:{possible}\:{sequences}? \\ $$$$ \\ $$
Commented by mr W last updated on 09/Aug/23

$${i}\:{got}\:\mathrm{9}.\mathrm{1}\:{in}\:{a}\:{tough}\:{way},\:{see}\:{below}. \\ $$$${do}\:{you}\:{also}\:{have}\:{a}\:{solution}? \\ $$
Commented by uchihayahia last updated on 09/Aug/23
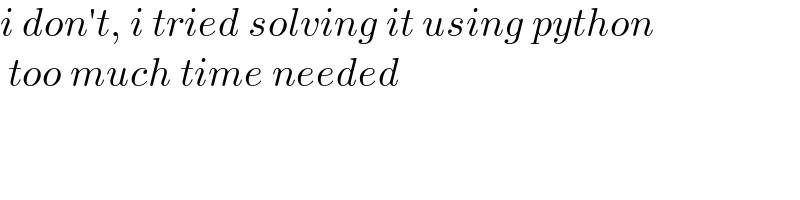
$${i}\:{don}'{t},\:{i}\:{tried}\:{solving}\:{it}\:{using}\:{python} \\ $$$$\:{too}\:{much}\:{time}\:{needed} \\ $$
Answered by mr W last updated on 09/Aug/23

$$\mathrm{7}\:``{a}''\:{and}\:\mathrm{13}\:``{b}'' \\ $$$${n}={orderly}\:{value} \\ $$$${n}_{{min}} =\mathrm{1} \\ $$$${n}_{{max}} =\mathrm{14} \\ $$$${in}\:{following} \\ $$$${A}\:{means}\:{a}\:{box}\:{containing}\:{one}\:{or}\: \\ $$$${more}\:{letters}\:``{a}'' \\ $$$${B}\:{means}\:{a}\:{box}\:{containing}\:{one}\:{or}\: \\ $$$${more}\:{letters}\:``{b}'' \\ $$$$ \\ $$$${n}=\mathrm{1}: \\ $$$${A}\mid{B}\:\Rightarrow\mathrm{1}\:{way} \\ $$$${B}\mid{A}\:\Rightarrow\mathrm{1}\:{way} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−−−\:\:\mathrm{2} \\ $$$${n}=\mathrm{2}: \\ $$$${A}\mid{B}\mid{A}\:\Rightarrow\:\mathrm{6}×\mathrm{1}=\mathrm{6}\:{ways} \\ $$$${B}\mid{A}\mid{B}\:\Rightarrow\:\mathrm{1}×\mathrm{12}=\mathrm{12}\:{ways} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−−−\:\mathrm{18} \\ $$$${n}=\mathrm{3}: \\ $$$${A}\mid{B}\mid{A}\:\mid{B}\Rightarrow\:\mathrm{6}×\mathrm{12}=\mathrm{72}\:{ways} \\ $$$${B}\mid{A}\mid{B}\:\mid{A}\Rightarrow\:\mathrm{6}×\mathrm{12}=\mathrm{72}\:{ways} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−−−\:\mathrm{144} \\ $$$${n}=\mathrm{4}: \\ $$$${A}\mid{B}\mid{A}\:\mid{B}\mid{A}\Rightarrow\:\mathrm{15}×\mathrm{12}=\mathrm{180}\:{ways} \\ $$$${B}\mid{A}\mid{B}\:\mid{A}\mid{B}\Rightarrow\:\mathrm{6}×\mathrm{66}=\:\mathrm{396}\:{ways} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−−−\:\mathrm{576} \\ $$$${n}=\mathrm{5}: \\ $$$${A}\mid{B}\:\mid{A}\mid{B}\mid{A}\mid{B}\Rightarrow\:\mathrm{15}×\mathrm{66}=\mathrm{990}\:{ways} \\ $$$${B}\mid{A}\mid{B}\:\mid{A}\mid{B}\mid{A}\Rightarrow\:\mathrm{15}×\mathrm{66}=\mathrm{990}\:{ways} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−−−\:\mathrm{1980} \\ $$$${n}=\mathrm{6}: \\ $$$${A}\mid{B}\:\mid{A}\mid{B}\mid{A}\mid{B}\mid{A}\Rightarrow\:\mathrm{20}×\mathrm{66}=\mathrm{1320}\:{ways} \\ $$$${B}\mid{A}\mid{B}\:\mid{A}\mid{B}\mid{A}\mid{B}\Rightarrow\:\mathrm{15}×\mathrm{220}=\mathrm{3300}\:{ways} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−−−\:\mathrm{4620} \\ $$$${n}=\mathrm{7}: \\ $$$${A}\mid{B}\:\mid{A}\mid{B}\mid{A}\mid{B}\mid{A}\mid{B}\Rightarrow\:\mathrm{20}×\mathrm{220}=\mathrm{4400}\:{ways} \\ $$$${B}\mid{A}\mid{B}\:\mid{A}\mid{B}\mid{A}\mid{B}\mid{A}\Rightarrow\:\mathrm{20}×\mathrm{220}=\mathrm{4400}\:{ways} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−−−\:\mathrm{8800} \\ $$$${n}=\mathrm{8}: \\ $$$${A}\mid{B}\:\mid{A}\mid{B}\mid{A}\mid{B}\mid{A}\mid{B}\mid{A}\Rightarrow\:\mathrm{15}×\mathrm{220}=\mathrm{3300}\:{ways} \\ $$$${B}\mid{A}\mid{B}\:\mid{A}\mid{B}\mid{A}\mid{B}\mid{A}\mid{B}\Rightarrow\:\mathrm{20}×\mathrm{495}=\mathrm{9900}\:{ways} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−−−\:\mathrm{13200} \\ $$$${n}=\mathrm{9}: \\ $$$${A}\mid{B}\:\mid{A}\mid{B}\mid{A}\mid{B}\mid{A}\mid{B}\mid{A}\mid{B}\Rightarrow\:\mathrm{15}×\mathrm{495}=\mathrm{7425}\:{ways} \\ $$$${B}\:\mid{A}\mid{B}\mid{A}\mid{B}\mid{A}\mid{B}\mid{A}\mid{B}\mid{A}\Rightarrow\:\mathrm{15}×\mathrm{495}=\mathrm{7425}\:{ways} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−−−\:\mathrm{14850} \\ $$$${n}=\mathrm{10}: \\ $$$${A}\mid{B}\:\mid{A}\mid{B}\mid{A}\mid{B}\mid{A}\mid{B}\mid{A}\mid{B}\mid{A}\Rightarrow\:\mathrm{6}×\mathrm{495}=\mathrm{2970}\:{ways} \\ $$$${B}\:\mid{A}\mid{B}\mid{A}\mid{B}\mid{A}\mid{B}\mid{A}\mid{B}\mid{A}\mid{B}\Rightarrow\:\mathrm{15}×\mathrm{792}=\mathrm{11880}\:{ways} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−−−\:\mathrm{14850} \\ $$$${n}=\mathrm{11}: \\ $$$${A}\mid{B}\:\mid{A}\mid{B}\mid{A}\mid{B}\mid{A}\mid{B}\mid{A}\mid{B}\mid{A}\mid{B}\Rightarrow\:\mathrm{6}×\mathrm{792}=\mathrm{4752}\:{ways} \\ $$$${B}\:\mid{A}\mid{B}\mid{A}\mid{B}\mid{A}\mid{B}\mid{A}\mid{B}\mid{A}\mid{B}\mid{A}\Rightarrow\:\mathrm{6}×\mathrm{792}=\mathrm{4752}\:{ways} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−−−\:\mathrm{9504} \\ $$$${n}=\mathrm{12}: \\ $$$${A}\mid{B}\:\mid{A}\mid{B}\mid{A}\mid{B}\mid{A}\mid{B}\mid{A}\mid{B}\mid{A}\mid{B}\mid{A}\Rightarrow\:\mathrm{1}×\mathrm{792}=\mathrm{792}\:{ways} \\ $$$${B}\:\mid{A}\mid{B}\mid{A}\mid{B}\mid{A}\mid{B}\mid{A}\mid{B}\mid{A}\mid{B}\mid{A}\mid{B}\Rightarrow\:\mathrm{6}×\mathrm{924}=\mathrm{5544}\:{ways} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−−−\:\mathrm{6336} \\ $$$${n}=\mathrm{13}: \\ $$$${A}\mid{B}\:\mid{A}\mid{B}\mid{A}\mid{B}\mid{A}\mid{B}\mid{A}\mid{B}\mid{A}\mid{B}\mid{A}\mid{B}\Rightarrow\:\mathrm{1}×\mathrm{924}=\mathrm{924}\:{ways} \\ $$$${B}\:\mid{A}\mid{B}\mid{A}\mid{B}\mid{A}\mid{B}\mid{A}\mid{B}\mid{A}\mid{B}\mid{A}\mid{B}\mid{A}\Rightarrow\:\mathrm{1}×\mathrm{924}=\mathrm{924}\:{ways} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−−−\:\mathrm{1848} \\ $$$${n}=\mathrm{14}: \\ $$$${B}\:\mid{A}\mid{B}\mid{A}\mid{B}\mid{A}\mid{B}\mid{A}\mid{B}\mid{A}\mid{B}\mid{A}\mid{B}\mid{A}\mid{B}\Rightarrow\:\mathrm{1}×\mathrm{792}=\mathrm{792}\:{ways} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−−−\:\mathrm{792} \\ $$$$ \\ $$$${mean}=\frac{\mathrm{2}×\mathrm{1}+\mathrm{18}×\mathrm{2}+\mathrm{144}×\mathrm{3}+\mathrm{576}×\mathrm{4}+\mathrm{1980}×\mathrm{5}+\mathrm{4620}×\mathrm{6}+\mathrm{8800}×\mathrm{7}+\mathrm{13200}×\mathrm{8}+\mathrm{14850}×\mathrm{9}+\mathrm{14850}×\mathrm{10}+\mathrm{9504}×\mathrm{11}+\mathrm{6336}×\mathrm{12}+\mathrm{1848}×\mathrm{13}+\mathrm{792}×\mathrm{14}}{\mathrm{2}+\mathrm{18}+\mathrm{144}+\mathrm{576}+\mathrm{1980}+\mathrm{4620}+\mathrm{8800}+\mathrm{13200}+\mathrm{14850}+\mathrm{14850}+\mathrm{9504}+\mathrm{6336}+\mathrm{1848}+\mathrm{792}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{705}\:\mathrm{432}}{\mathrm{77}\:\mathrm{520}}=\mathrm{9}.\mathrm{1}\:\checkmark \\ $$$$ \\ $$$${check}: \\ $$$${number}\:{of}\:{total}\:{possibilities}\: \\ $$$$=\frac{\mathrm{20}!}{\mathrm{7}!×\mathrm{13}!}=\mathrm{77}\:\mathrm{520}\:\checkmark \\ $$
Commented by uchihayahia last updated on 09/Aug/23

$$\:{thanks}\:{you},\:{i}'{ll}\:{do}\:{my}\:{best}\:{to}\:{understand}\:{your} \\ $$$$\:{answer}.\:{still}\:{studying}\:{basic}\:{combinatrics}\: \\ $$
Commented by mr W last updated on 09/Aug/23

$${i}'{ll}\:{give}\:{some}\:{explanation}\:{for}\:{my} \\ $$$${solution}. \\ $$$${example}:\:\:{the}\:{orderly}\:{value}\:{is}\:{n}=\mathrm{4}.\: \\ $$$${that}\:{means}\:{there}\:{are}\:\mathrm{4} \\ $$$${places}\:{where}\:{a}\:``{a}''\:{and}\:{a}\:``{b}''\:{are} \\ $$$${next}\:{to}\:{each}\:{other}.\:{such}\:{a}\:{place}\:{is} \\ $$$${marked}\:{as}\:``\mid''.\:{we}\:{have}\:{two}\:{cases}: \\ $$$${case}\:\mathrm{1}:\:{A}\mid{B}\mid{A}\:\mid{B}\mid{A} \\ $$$${to}\:{distribute}\:\mathrm{7}\:``{a}''\:{in}\:\mathrm{3}\:{boxes}\:{there}\:{are} \\ $$$${C}_{\mathrm{7}−\mathrm{1}} ^{\mathrm{3}−\mathrm{1}} =\mathrm{15}\:{ways} \\ $$$${to}\:{distribute}\:\mathrm{13}\:``{b}''\:{in}\:\mathrm{2}\:{boxes}\:{there}\:{are} \\ $$$${C}_{\mathrm{13}−\mathrm{1}} ^{\mathrm{2}−\mathrm{1}} =\mathrm{12}\:{ways} \\ $$$$\Rightarrow\:{totally}\:\mathrm{15}×\mathrm{12}=\mathrm{180}\:{ways} \\ $$$${case}\:\mathrm{2}:\:{B}\mid{A}\mid{B}\:\mid{A}\mid{B} \\ $$$${to}\:{distribute}\:\mathrm{7}\:``{a}''\:{in}\:\mathrm{2}\:{boxes}\:{there}\:{are} \\ $$$${C}_{\mathrm{7}−\mathrm{1}} ^{\mathrm{2}−\mathrm{1}} =\mathrm{6}\:{ways} \\ $$$${to}\:{distribute}\:\mathrm{13}\:``{b}''\:{in}\:\mathrm{3}\:{boxes}\:{there}\:{are} \\ $$$${C}_{\mathrm{13}−\mathrm{1}} ^{\mathrm{3}−\mathrm{1}} =\mathrm{66}\:{ways} \\ $$$$\Rightarrow{totally}\:\:\mathrm{6}×\mathrm{66}=\:\mathrm{396}\:{ways} \\ $$$${therefore}\:{there}\:{are}\:\mathrm{180}+\mathrm{396}=\mathrm{576}\: \\ $$$${possibilities}\:{for}\:{the}\:{orderly}\:{value}\:\mathrm{4}. \\ $$
Commented by uchihayahia last updated on 11/Aug/23
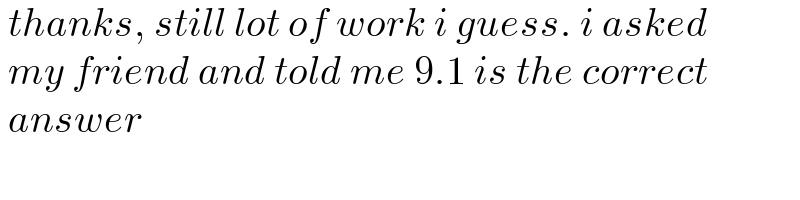
$$\:{thanks},\:{still}\:{lot}\:{of}\:{work}\:{i}\:{guess}.\:{i}\:{asked} \\ $$$$\:{my}\:{friend}\:{and}\:{told}\:{me}\:\mathrm{9}.\mathrm{1}\:{is}\:{the}\:{correct} \\ $$$$\:{answer} \\ $$
Commented by mr W last updated on 11/Aug/23
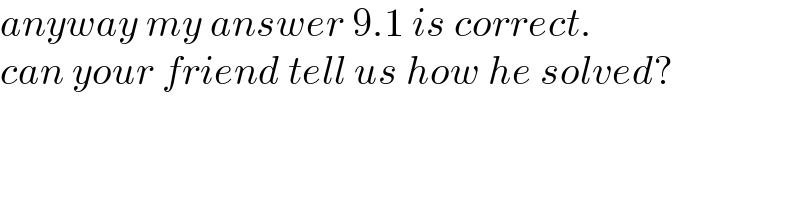
$${anyway}\:{my}\:{answer}\:\mathrm{9}.\mathrm{1}\:{is}\:{correct}. \\ $$$${can}\:{your}\:{friend}\:{tell}\:{us}\:{how}\:{he}\:{solved}? \\ $$
Commented by uchihayahia last updated on 12/Aug/23
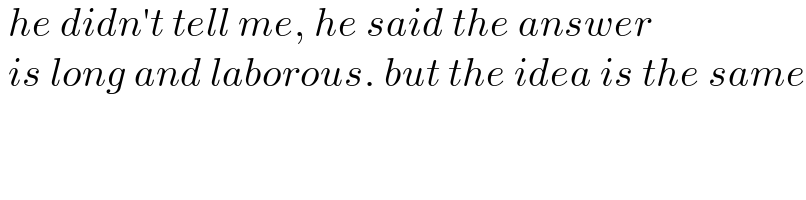
$$\:{he}\:{didn}'{t}\:{tell}\:{me},\:{he}\:{said}\:{the}\:{answer} \\ $$$$\:{is}\:{long}\:{and}\:{laborous}.\:{but}\:{the}\:{idea}\:{is}\:{the}\:{same} \\ $$
Commented by mr W last updated on 12/Aug/23
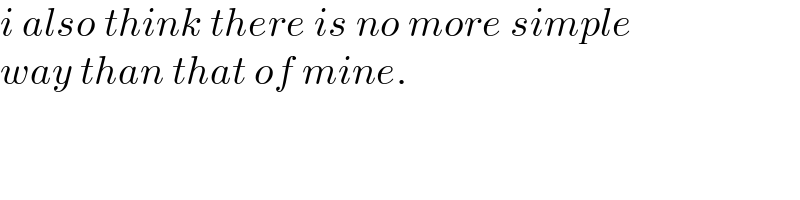
$${i}\:{also}\:{think}\:{there}\:{is}\:{no}\:{more}\:{simple} \\ $$$${way}\:{than}\:{that}\:{of}\:{mine}. \\ $$
