
Question Number 195619 by cortano12 last updated on 06/Aug/23

$$\:\:\:\cancel{\underline{\underbrace{ }}} \\ $$
Answered by MM42 last updated on 06/Aug/23

$$\infty \\ $$
Answered by dimentri last updated on 06/Aug/23
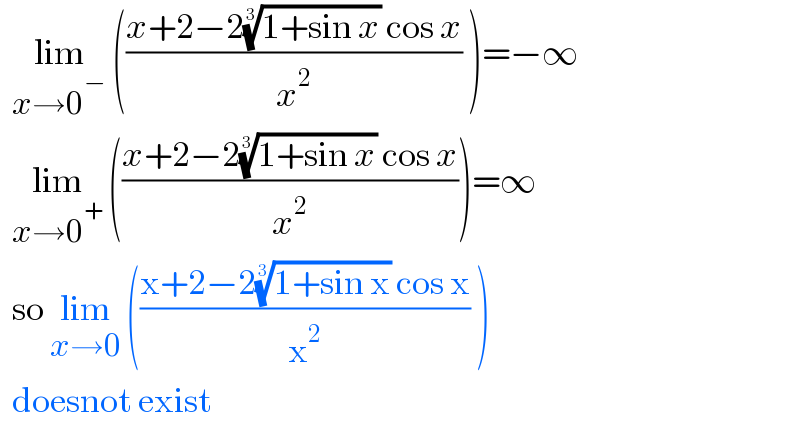
$$\:\:\underset{{x}\rightarrow\mathrm{0}^{−} } {\mathrm{lim}}\:\left(\frac{{x}+\mathrm{2}−\mathrm{2}\sqrt[{\mathrm{3}}]{\mathrm{1}+\mathrm{sin}\:{x}}\:\mathrm{cos}\:{x}}{{x}^{\mathrm{2}} }\:\right)=−\infty \\ $$$$\:\:\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\left(\frac{{x}+\mathrm{2}−\mathrm{2}\sqrt[{\mathrm{3}}]{\mathrm{1}+\mathrm{sin}\:{x}}\:\mathrm{cos}\:{x}}{{x}^{\mathrm{2}} }\right)=\infty \\ $$$$\:\:\mathrm{so}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\mathrm{x}+\mathrm{2}−\mathrm{2}\sqrt[{\mathrm{3}}]{\mathrm{1}+\mathrm{sin}\:\mathrm{x}}\:\mathrm{cos}\:\mathrm{x}}{\mathrm{x}^{\mathrm{2}} }\:\right) \\ $$$$\:\:\mathrm{doesnot}\:\mathrm{exist}\: \\ $$
