
Question Number 195540 by 073 last updated on 04/Aug/23
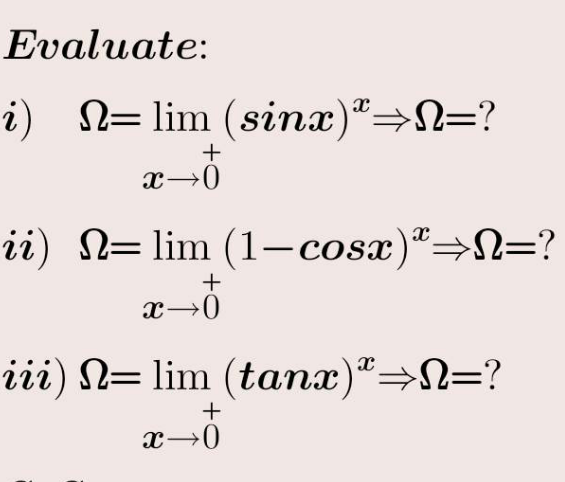
Commented by Frix last updated on 04/Aug/23

$$\left.{i}\right)\:\mathrm{1} \\ $$$$\left.{ii}\right)\:\mathrm{1} \\ $$$$\left.{iii}\right)\:\mathrm{1} \\ $$
Commented by 073 last updated on 04/Aug/23

$$\mathrm{prove}\:\mathrm{please}? \\ $$
Answered by MM42 last updated on 05/Aug/23
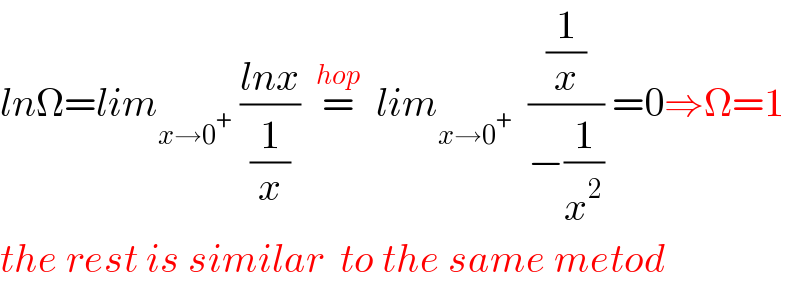
$${ln}\Omega={lim}_{{x}\rightarrow\mathrm{0}^{+} } \:\frac{{lnx}}{\frac{\mathrm{1}}{{x}}}\:\:\overset{{hop}} {=}\:\:{lim}_{{x}\rightarrow\mathrm{0}^{+} } \:\:\frac{\frac{\mathrm{1}}{{x}}}{−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}\:=\mathrm{0}\Rightarrow\Omega=\mathrm{1} \\ $$$${the}\:{rest}\:{is}\:{similar}\:\:{to}\:{the}\:{same}\:{metod} \\ $$
