
Question Number 195520 by moh777 last updated on 04/Aug/23
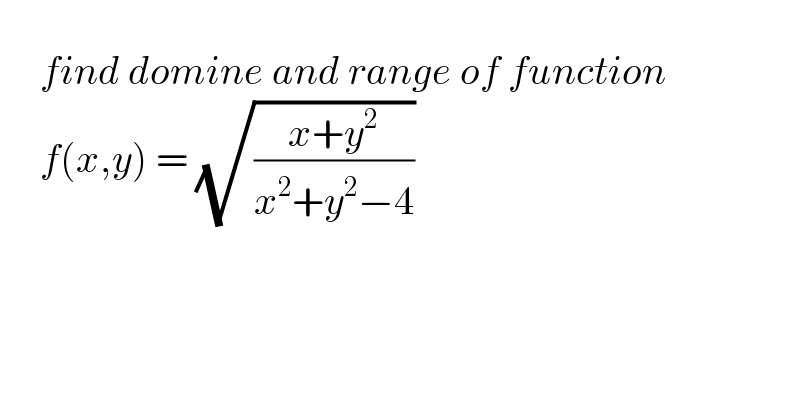
$$\: \\ $$$$\:\:\:\:\:{find}\:{domine}\:{and}\:{range}\:{of}\:{function}\: \\ $$$$\:\:\:\:\:{f}\left({x},{y}\right)\:=\:\sqrt{\frac{{x}+{y}^{\mathrm{2}} }{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{4}}} \\ $$$$ \\ $$$$ \\ $$
Answered by MM42 last updated on 04/Aug/23
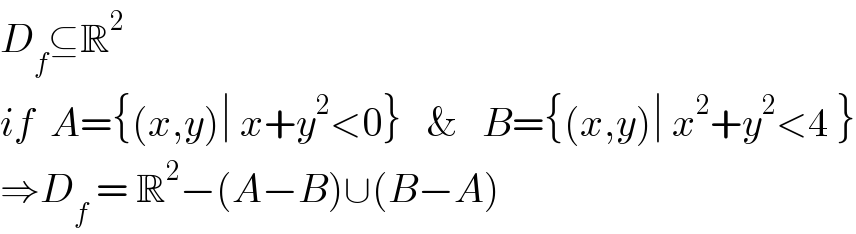
$${D}_{{f}} \subseteq\mathbb{R}^{\mathrm{2}} \:\: \\ $$$${if}\:\:{A}=\left\{\left({x},{y}\right)\mid\:{x}+{y}^{\mathrm{2}} <\mathrm{0}\right\}\:\:\:\&\:\:\:{B}=\left\{\left({x},{y}\right)\mid\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} <\mathrm{4}\:\right\} \\ $$$$\Rightarrow{D}_{{f}} \:=\:\mathbb{R}^{\mathrm{2}} −\left({A}−{B}\right)\cup\left({B}−{A}\right) \\ $$
Answered by witcher3 last updated on 04/Aug/23
![(x,y)→((x+y^2 )/(x^2 +y^2 −4)) is continus (x,y)=(rcos(a),rsin(a)) r∈[0,∞[ ,a∈[0,2π]r f(x,y)=f(rcos(a),rsin(a))=g(r,a) =(√((rcos(a)+r^2 sin^2 (a))/(r^2 −4))) for r>2,a∈[0,(π/2)] g is well defind g(0,0 lim_(r→∞) g(r,a)=0 lim_(r→2^+ ) g(r,a)=+∞ ⇒range f is ]0,+∞[ 0=g(0,a) range is [0,∞[](Q195528.png)
$$\left(\mathrm{x},\mathrm{y}\right)\rightarrow\frac{\mathrm{x}+\mathrm{y}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} −\mathrm{4}}\:\mathrm{is}\:\mathrm{continus} \\ $$$$\left(\mathrm{x},\mathrm{y}\right)=\left(\mathrm{rcos}\left(\mathrm{a}\right),\mathrm{rsin}\left(\mathrm{a}\right)\right) \\ $$$$\mathrm{r}\in\left[\mathrm{0},\infty\left[\:,\mathrm{a}\in\left[\mathrm{0},\mathrm{2}\pi\right]\mathrm{r}\right.\right. \\ $$$$\mathrm{f}\left(\mathrm{x},\mathrm{y}\right)=\mathrm{f}\left(\mathrm{rcos}\left(\mathrm{a}\right),\mathrm{rsin}\left(\mathrm{a}\right)\right)=\mathrm{g}\left(\mathrm{r},\mathrm{a}\right) \\ $$$$=\sqrt{\frac{\mathrm{rcos}\left(\mathrm{a}\right)+\mathrm{r}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \left(\mathrm{a}\right)}{\mathrm{r}^{\mathrm{2}} −\mathrm{4}}} \\ $$$$\mathrm{for}\:\mathrm{r}>\mathrm{2},\mathrm{a}\in\left[\mathrm{0},\frac{\pi}{\mathrm{2}}\right]\:\mathrm{g}\:\mathrm{is}\:\mathrm{well}\:\mathrm{defind} \\ $$$$\mathrm{g}\left(\mathrm{0},\mathrm{0}\right. \\ $$$$\underset{\mathrm{r}\rightarrow\infty} {\mathrm{lim}g}\left(\mathrm{r},\mathrm{a}\right)=\mathrm{0} \\ $$$$\underset{\mathrm{r}\rightarrow\mathrm{2}^{+} } {\mathrm{lim}g}\left(\mathrm{r},\mathrm{a}\right)=+\infty \\ $$$$\left.\Rightarrow\mathrm{range}\:\mathrm{f}\:\mathrm{is}\:\right]\mathrm{0},+\infty\left[\right. \\ $$$$\mathrm{0}=\mathrm{g}\left(\mathrm{0},\mathrm{a}\right)\:\mathrm{range}\:\mathrm{is}\:\left[\mathrm{0},\infty\left[\right.\right. \\ $$
Answered by Frix last updated on 04/Aug/23
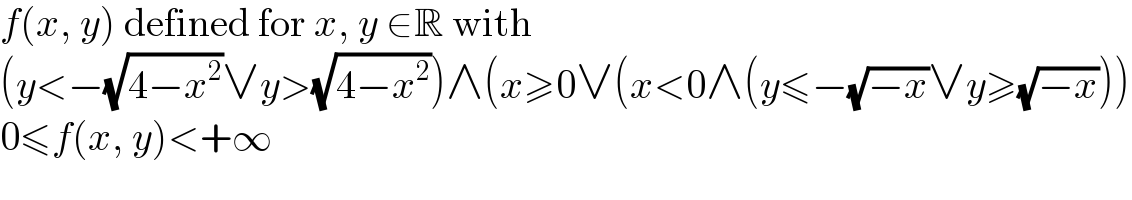
$${f}\left({x},\:{y}\right)\:\mathrm{defined}\:\mathrm{for}\:{x},\:{y}\:\in\mathbb{R}\:\mathrm{with} \\ $$$$\left({y}<−\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }\vee{y}>\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }\right)\wedge\left({x}\geqslant\mathrm{0}\vee\left({x}<\mathrm{0}\wedge\left({y}\leqslant−\sqrt{−{x}}\vee{y}\geqslant\sqrt{−{x}}\right)\right)\right. \\ $$$$\mathrm{0}\leqslant{f}\left({x},\:{y}\right)<+\infty \\ $$
