
Question Number 195517 by cortano12 last updated on 04/Aug/23
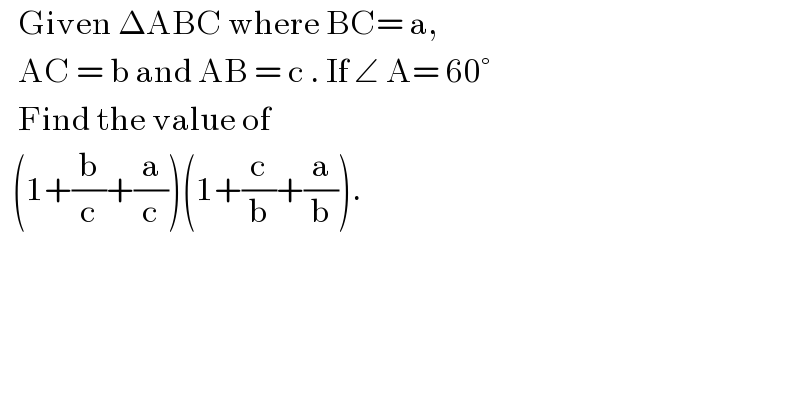
$$\:\:\:\mathrm{Given}\:\Delta\mathrm{ABC}\:\mathrm{where}\:\mathrm{BC}=\:\mathrm{a},\: \\ $$$$\:\:\:\mathrm{AC}\:=\:\mathrm{b}\:\mathrm{and}\:\mathrm{AB}\:=\:\mathrm{c}\:.\:\mathrm{If}\:\angle\:\mathrm{A}=\:\mathrm{60}° \\ $$$$\:\:\:\mathrm{Find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\: \\ $$$$\:\:\left(\mathrm{1}+\frac{\mathrm{b}}{\mathrm{c}}+\frac{\mathrm{a}}{\mathrm{c}}\right)\left(\mathrm{1}+\frac{\mathrm{c}}{\mathrm{b}}+\frac{\mathrm{a}}{\mathrm{b}}\right). \\ $$$$ \\ $$
Answered by horsebrand11 last updated on 05/Aug/23
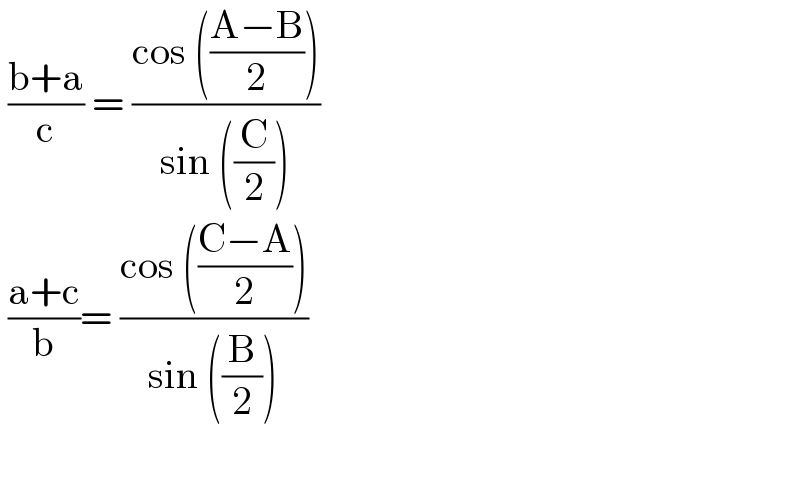
$$\:\frac{\mathrm{b}+\mathrm{a}}{\mathrm{c}}\:=\:\frac{\mathrm{cos}\:\left(\frac{\mathrm{A}−\mathrm{B}}{\mathrm{2}}\right)}{\mathrm{sin}\:\left(\frac{\mathrm{C}}{\mathrm{2}}\right)} \\ $$$$\:\frac{\mathrm{a}+\mathrm{c}}{\mathrm{b}}=\:\frac{\mathrm{cos}\:\left(\frac{\mathrm{C}−\mathrm{A}}{\mathrm{2}}\right)}{\mathrm{sin}\:\left(\frac{\mathrm{B}}{\mathrm{2}}\right)} \\ $$$$\: \\ $$
