
Question Number 195454 by universe last updated on 02/Aug/23
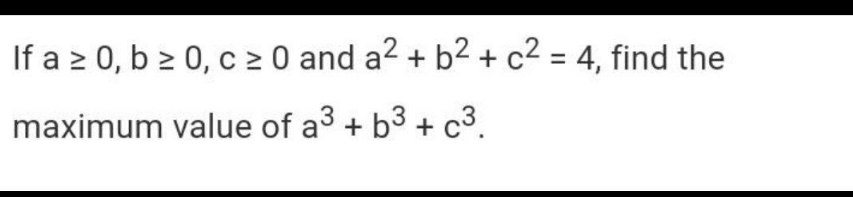
Commented by mr W last updated on 03/Aug/23
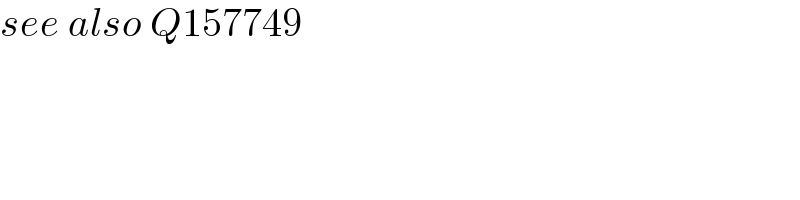
$${see}\:{also}\:{Q}\mathrm{157749} \\ $$
Answered by Frix last updated on 03/Aug/23

$${a}=\mathrm{2}\:{b}={c}=\mathrm{0} \\ $$$$\mathrm{2}^{\mathrm{3}} =\mathrm{8} \\ $$
Commented by universe last updated on 03/Aug/23
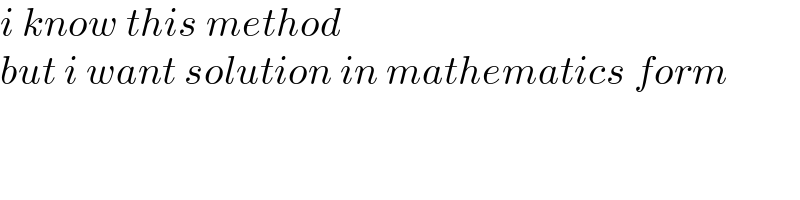
$${i}\:{know}\:{this}\:{method}\: \\ $$$${but}\:{i}\:{want}\:{solution}\:{in}\:{mathematics}\:{form} \\ $$
Answered by witcher3 last updated on 03/Aug/23

$$\mathrm{use}\:\sqrt[{\mathrm{q}}]{\frac{\underset{\mathrm{i}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\mathrm{x}_{\mathrm{i}} ^{\mathrm{q}} }{\mathrm{n}}}=\mathrm{f}\left(\mathrm{q}\right)\:\mathrm{increse}\:\mathrm{function}\: \\ $$$$\Rightarrow\sqrt[{\mathrm{3}}]{\frac{\mathrm{a}^{\mathrm{3}} +\mathrm{b}^{\mathrm{3}} +\mathrm{c}^{\mathrm{3}} }{\mathrm{3}}}\geqslant\left(\frac{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} }{\mathrm{3}}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} =\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}} \\ $$$$\Rightarrow\mathrm{a}^{\mathrm{3}} +\mathrm{b}^{\mathrm{3}} +\mathrm{c}^{\mathrm{2}} \geqslant\frac{\mathrm{8}}{\mathrm{3}\sqrt{\mathrm{3}}}.\mathrm{3}=\frac{\mathrm{8}}{\:\sqrt{\mathrm{3}}} \\ $$$$\mathrm{a}=\mathrm{b}=\mathrm{c}\Rightarrow\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}} \\ $$$$ \\ $$
Commented by deleteduser1 last updated on 03/Aug/23
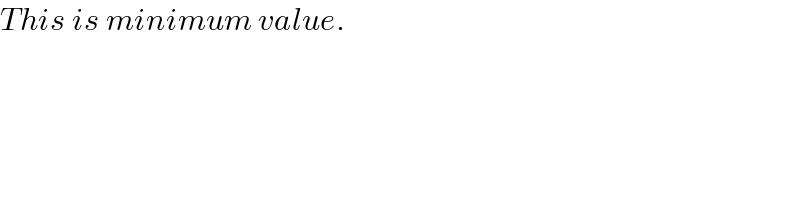
$${This}\:{is}\:{minimum}\:{value}. \\ $$
Commented by witcher3 last updated on 03/Aug/23

$$\mathrm{yes}\:\mathrm{i}\:\mathrm{dont}\:\mathrm{know}\:\mathrm{why}\:\mathrm{in}\:\mathrm{my}\:\mathrm{mind}\:\mathrm{this}\:\mathrm{is}\:\mathrm{the}\:\mathrm{Quation} \\ $$
Answered by witcher3 last updated on 03/Aug/23
![a^3 +b^3 +c^3 =4((a^3 /(a^2 +b^2 +c^2 ))+(b^3 /(a^2 +b^2 +c^2 ))+(c^3 /(a^2 +b^2 +c^3 ))) =4(((a^3 +b^3 +c^3 )/(b^2 +c^2 +a^2 ))) M∈R_+ ,a^3 +b^3 +c^3 ≤M(a^2 +b^2 +c^2 ) M=max {a,b,c}=a;a^3 +b^3 +c^3 ≤a^3 +a(b^2 +c^2 ) true if a≥1 a^2 +b^2 +c^2 ≤3max{a^2 ,b^2 ,c^2 } max{a^2 ,b^2 ,c^2 }=max^2 {a,b,c}≥(4/3)⇒m≥(2/( (√3)))>1.. True ,hence Get idea if one of a,b,c Get bigger a^3 +b^3 +c^3 get bigger a=2,b=c=0 a^3 +b^3 +c^3 =8 a^3 +b^3 +c^3 ≤8...∀(a,b,c)∣a^2 +b^2 +c^2 =4⇒(a,b,c)∈[0,2]^2 8=2(a^2 +b^2 +c^2 ) a^3 +b^3 +c^3 =a.a^2 +b.b^2 +c.c^2 ≤2a^2 +2b^2 +2c^2 =2(a^2 +b^2 +c^2 )=8](Q195486.png)
$$\mathrm{a}^{\mathrm{3}} +\mathrm{b}^{\mathrm{3}} +\mathrm{c}^{\mathrm{3}} =\mathrm{4}\left(\frac{\mathrm{a}^{\mathrm{3}} }{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} }+\frac{\mathrm{b}^{\mathrm{3}} }{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} }+\frac{\mathrm{c}^{\mathrm{3}} }{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{3}} }\right) \\ $$$$=\mathrm{4}\left(\frac{\mathrm{a}^{\mathrm{3}} +\mathrm{b}^{\mathrm{3}} +\mathrm{c}^{\mathrm{3}} }{\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} }\right) \\ $$$$\mathrm{M}\in\mathbb{R}_{+} ,\mathrm{a}^{\mathrm{3}} +\mathrm{b}^{\mathrm{3}} +\mathrm{c}^{\mathrm{3}} \leqslant\mathrm{M}\left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} \right) \\ $$$$\mathrm{M}=\mathrm{max}\:\left\{\mathrm{a},\mathrm{b},\mathrm{c}\right\}=\mathrm{a};\mathrm{a}^{\mathrm{3}} +\mathrm{b}^{\mathrm{3}} +\mathrm{c}^{\mathrm{3}} \leqslant\mathrm{a}^{\mathrm{3}} +\mathrm{a}\left(\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} \right) \\ $$$$\mathrm{true}\:\mathrm{if}\:\mathrm{a}\geqslant\mathrm{1} \\ $$$$\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} \leqslant\mathrm{3max}\left\{\mathrm{a}^{\mathrm{2}} ,\mathrm{b}^{\mathrm{2}} ,\mathrm{c}^{\mathrm{2}} \right\} \\ $$$$\mathrm{max}\left\{\mathrm{a}^{\mathrm{2}} ,\mathrm{b}^{\mathrm{2}} ,\mathrm{c}^{\mathrm{2}} \right\}=\mathrm{max}^{\mathrm{2}} \left\{\mathrm{a},\mathrm{b},\mathrm{c}\right\}\geqslant\frac{\mathrm{4}}{\mathrm{3}}\Rightarrow\mathrm{m}\geqslant\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}>\mathrm{1}.. \\ $$$$\mathrm{True}\:,\mathrm{hence}\:\mathrm{Get}\:\mathrm{idea}\:\mathrm{if}\:\mathrm{one}\:\mathrm{of}\:\mathrm{a},\mathrm{b},\mathrm{c}\:\mathrm{Get}\:\mathrm{bigger} \\ $$$$\mathrm{a}^{\mathrm{3}} +\mathrm{b}^{\mathrm{3}} +\mathrm{c}^{\mathrm{3}} \:\mathrm{get}\:\mathrm{bigger} \\ $$$$\mathrm{a}=\mathrm{2},\mathrm{b}=\mathrm{c}=\mathrm{0} \\ $$$$\mathrm{a}^{\mathrm{3}} +\mathrm{b}^{\mathrm{3}} +\mathrm{c}^{\mathrm{3}} =\mathrm{8} \\ $$$$\mathrm{a}^{\mathrm{3}} +\mathrm{b}^{\mathrm{3}} +\mathrm{c}^{\mathrm{3}} \leqslant\mathrm{8}...\forall\left(\mathrm{a},\mathrm{b},\mathrm{c}\right)\mid\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} =\mathrm{4}\Rightarrow\left(\mathrm{a},\mathrm{b},\mathrm{c}\right)\in\left[\mathrm{0},\mathrm{2}\right]^{\mathrm{2}} \\ $$$$\mathrm{8}=\mathrm{2}\left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} \right) \\ $$$$\mathrm{a}^{\mathrm{3}} +\mathrm{b}^{\mathrm{3}} +\mathrm{c}^{\mathrm{3}} =\mathrm{a}.\mathrm{a}^{\mathrm{2}} +\mathrm{b}.\mathrm{b}^{\mathrm{2}} +\mathrm{c}.\mathrm{c}^{\mathrm{2}} \leqslant\mathrm{2a}^{\mathrm{2}} +\mathrm{2b}^{\mathrm{2}} +\mathrm{2c}^{\mathrm{2}} =\mathrm{2}\left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} \right)=\mathrm{8} \\ $$$$ \\ $$$$\: \\ $$
Answered by universe last updated on 04/Aug/23
![LET a= 2sin α cos β b = 2 sin α sin β c = 2 cos α a^3 + b^3 +c^(3 ) = 8[sin^3 α(cos^3 β + sin^3 β)+cos^3 α]_(max = 1) max(a^3 +b^3 +c^3 ) = 8](Q195516.png)
$${LET} \\ $$$$\:{a}=\:\mathrm{2sin}\:\alpha\:\mathrm{cos}\:\beta \\ $$$$\:{b}\:=\:\mathrm{2}\:\mathrm{sin}\:\alpha\:\mathrm{sin}\:\beta \\ $$$$\:{c}\:=\:\mathrm{2}\:\mathrm{cos}\:\alpha \\ $$$${a}^{\mathrm{3}} +\:{b}^{\mathrm{3}} +{c}^{\mathrm{3}\:} \:=\:\:\mathrm{8}\underset{{max}\:=\:\mathrm{1}} {\underbrace{\left[\mathrm{sin}^{\mathrm{3}} \alpha\left(\mathrm{cos}^{\mathrm{3}} \beta\:+\:\mathrm{sin}^{\mathrm{3}} \beta\right)+\mathrm{cos}^{\mathrm{3}} \alpha\right]}} \\ $$$$\:\:\:\:{max}\left({a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} \right)\:\:=\:\mathrm{8} \\ $$$$\:\:\:\: \\ $$
