Question and Answers Forum

All Questions      Topic List

Differential Equation Questions

Previous in All Question      Next in All Question      

Previous in Differential Equation      Next in Differential Equation      

Question Number 195301 by deleteduser4 last updated on 29/Jul/23

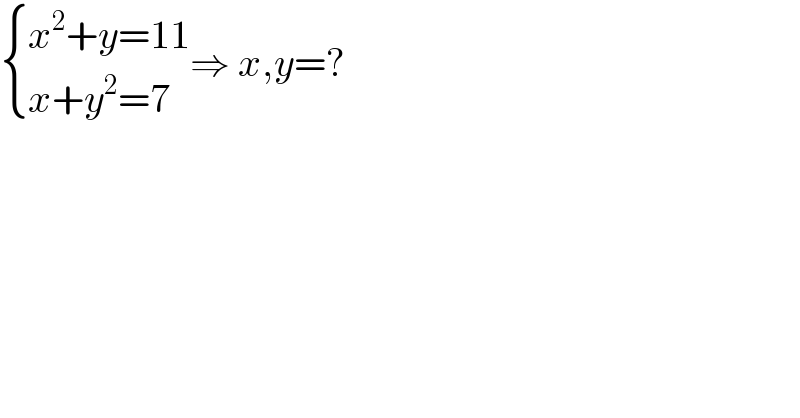
{ ((x^2 +y=11)),((x+y^2 =7)) :}⇒ x,y=?

$$\begin{cases}{{x}^{\mathrm{2}} +{y}=\mathrm{11}}\\{{x}+{y}^{\mathrm{2}} =\mathrm{7}}\end{cases}\Rightarrow\:{x},{y}=? \\ $$

Answered by Frix last updated on 29/Jul/23

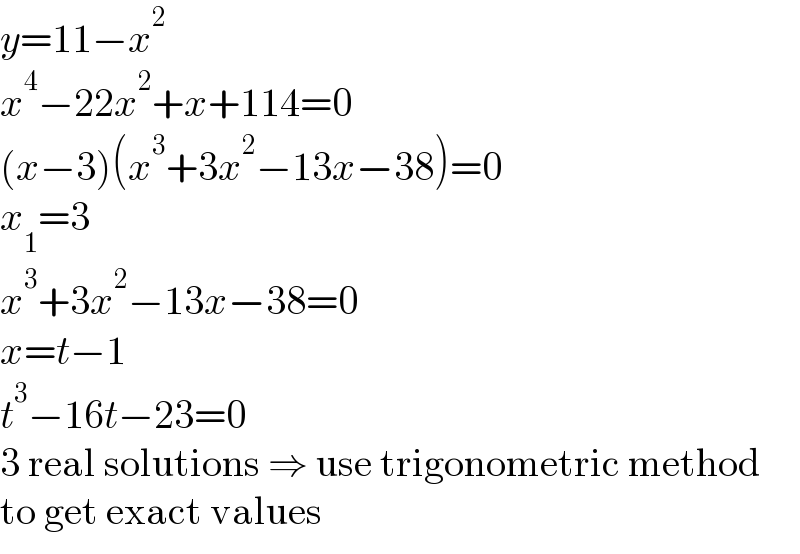
y=11−x^2 x^4 −22x^2 +x+114=0 (x−3)(x^3 +3x^2 −13x−38)=0 x_1 =3 x^3 +3x^2 −13x−38=0 x=t−1 t^3 −16t−23=0 3 real solutions ⇒ use trigonometric method to get exact values

$${y}=\mathrm{11}−{x}^{\mathrm{2}} \\ $$$${x}^{\mathrm{4}} −\mathrm{22}{x}^{\mathrm{2}} +{x}+\mathrm{114}=\mathrm{0} \\ $$$$\left({x}−\mathrm{3}\right)\left({x}^{\mathrm{3}} +\mathrm{3}{x}^{\mathrm{2}} −\mathrm{13}{x}−\mathrm{38}\right)=\mathrm{0} \\ $$$${x}_{\mathrm{1}} =\mathrm{3} \\ $$$${x}^{\mathrm{3}} +\mathrm{3}{x}^{\mathrm{2}} −\mathrm{13}{x}−\mathrm{38}=\mathrm{0} \\ $$$${x}={t}−\mathrm{1} \\ $$$${t}^{\mathrm{3}} −\mathrm{16}{t}−\mathrm{23}=\mathrm{0} \\ $$$$\mathrm{3}\:\mathrm{real}\:\mathrm{solutions}\:\Rightarrow\:\mathrm{use}\:\mathrm{trigonometric}\:\mathrm{method} \\ $$$$\mathrm{to}\:\mathrm{get}\:\mathrm{exact}\:\mathrm{values} \\ $$

Commented by deleteduser4 last updated on 29/Jul/23

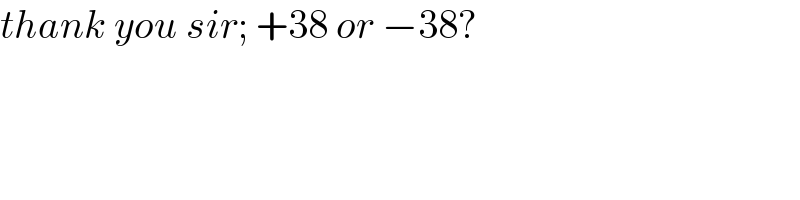
thank you sir; +38 or −38?

$${thank}\:{you}\:{sir};\:+\mathrm{38}\:{or}\:−\mathrm{38}? \\ $$

Commented by Frix last updated on 29/Jul/23

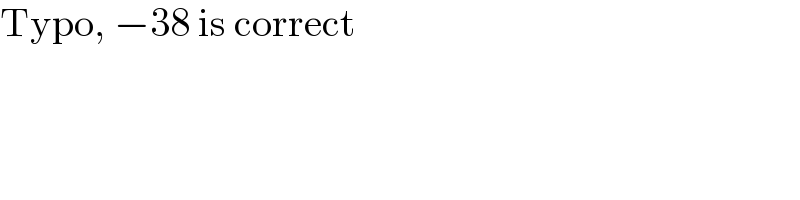
Typo, −38 is correct

$$\mathrm{Typo},\:−\mathrm{38}\:\mathrm{is}\:\mathrm{correct} \\ $$

Commented by Frix last updated on 29/Jul/23

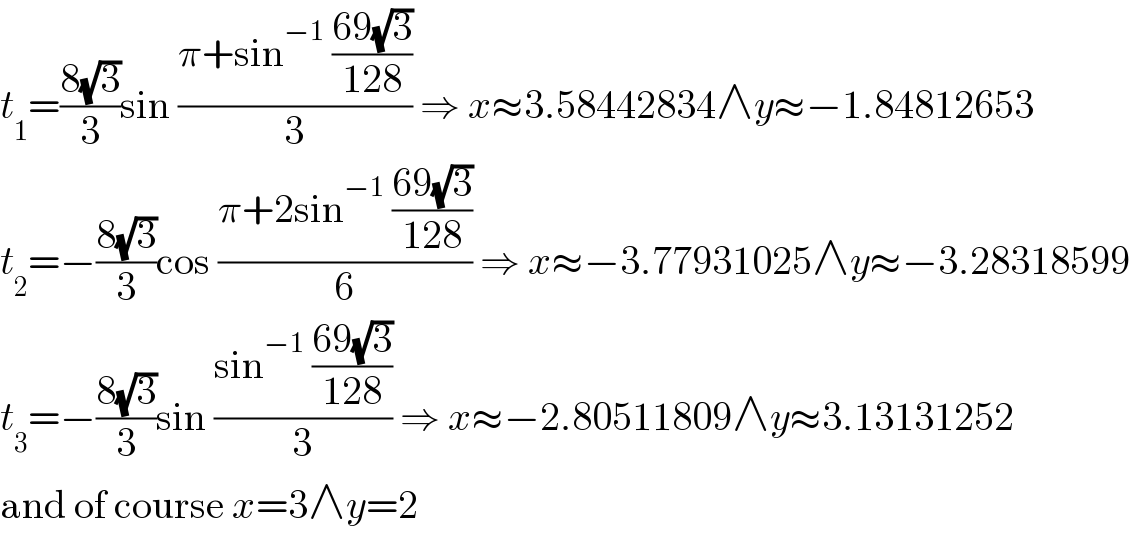
t_1 =((8(√3))/3)sin ((π+sin^(−1) ((69(√3))/(128)))/3) ⇒ x≈3.58442834∧y≈−1.84812653 t_2 =−((8(√3))/3)cos ((π+2sin^(−1) ((69(√3))/(128)))/6) ⇒ x≈−3.77931025∧y≈−3.28318599 t_3 =−((8(√3))/3)sin ((sin^(−1) ((69(√3))/(128)))/3) ⇒ x≈−2.80511809∧y≈3.13131252 and of course x=3∧y=2

$${t}_{\mathrm{1}} =\frac{\mathrm{8}\sqrt{\mathrm{3}}}{\mathrm{3}}\mathrm{sin}\:\frac{\pi+\mathrm{sin}^{−\mathrm{1}} \:\frac{\mathrm{69}\sqrt{\mathrm{3}}}{\mathrm{128}}}{\mathrm{3}}\:\Rightarrow\:{x}\approx\mathrm{3}.\mathrm{58442834}\wedge{y}\approx−\mathrm{1}.\mathrm{84812653} \\ $$$${t}_{\mathrm{2}} =−\frac{\mathrm{8}\sqrt{\mathrm{3}}}{\mathrm{3}}\mathrm{cos}\:\frac{\pi+\mathrm{2sin}^{−\mathrm{1}} \:\frac{\mathrm{69}\sqrt{\mathrm{3}}}{\mathrm{128}}}{\mathrm{6}}\:\Rightarrow\:{x}\approx−\mathrm{3}.\mathrm{77931025}\wedge{y}\approx−\mathrm{3}.\mathrm{28318599} \\ $$$${t}_{\mathrm{3}} =−\frac{\mathrm{8}\sqrt{\mathrm{3}}}{\mathrm{3}}\mathrm{sin}\:\frac{\mathrm{sin}^{−\mathrm{1}} \:\frac{\mathrm{69}\sqrt{\mathrm{3}}}{\mathrm{128}}}{\mathrm{3}}\:\Rightarrow\:{x}\approx−\mathrm{2}.\mathrm{80511809}\wedge{y}\approx\mathrm{3}.\mathrm{13131252} \\ $$$$\mathrm{and}\:\mathrm{of}\:\mathrm{course}\:{x}=\mathrm{3}\wedge{y}=\mathrm{2} \\ $$

Commented by deleteduser4 last updated on 29/Jul/23

very very nice sir; and infinity thank you

$${very}\:{very}\:{nice}\:{sir};\:{and}\:{infinity}\:{thank}\:{you} \\ $$

Commented by Frix last updated on 30/Jul/23

To clarify: t^3 +pt+q=0 If (p^3 /(27))+(q^2 /4)<0 Cardano doesn′t work. This is even wrong in wolframalpha. We need the Trigonometric Method leading to t_k =((2(√(−3p)))/3)sin ((2kπ+sin^(−1) ((3(√3)q)/(2(√(−p^3 )))))/3) with k=1, 2, 3

$$\mathrm{To}\:\mathrm{clarify}: \\ $$$${t}^{\mathrm{3}} +{pt}+{q}=\mathrm{0} \\ $$$$\mathrm{If}\:\frac{{p}^{\mathrm{3}} }{\mathrm{27}}+\frac{{q}^{\mathrm{2}} }{\mathrm{4}}<\mathrm{0}\:\mathrm{Cardano}\:\mathrm{doesn}'\mathrm{t}\:\mathrm{work}.\:\mathrm{This} \\ $$$$\mathrm{is}\:\mathrm{even}\:\mathrm{wrong}\:\mathrm{in}\:\mathrm{wolframalpha}.\:\mathrm{We}\:\mathrm{need} \\ $$$$\mathrm{the}\:\mathrm{Trigonometric}\:\mathrm{Method}\:\mathrm{leading}\:\mathrm{to} \\ $$$${t}_{{k}} =\frac{\mathrm{2}\sqrt{−\mathrm{3}{p}}}{\mathrm{3}}\mathrm{sin}\:\frac{\mathrm{2}{k}\pi+\mathrm{sin}^{−\mathrm{1}} \:\frac{\mathrm{3}\sqrt{\mathrm{3}}{q}}{\mathrm{2}\sqrt{−{p}^{\mathrm{3}} }}}{\mathrm{3}}\:\mathrm{with}\:{k}=\mathrm{1},\:\mathrm{2},\:\mathrm{3} \\ $$

Commented by Frix last updated on 30/Jul/23

My solution proves there are 4 real intersections. It′s obviously a problem of the approximation. An imaginary part of ≈.0000000000000001i is strange. But as I wrote before, your picture also shows 4 real solutions. Do you trust more in an algorithm?

$$\mathrm{My}\:\mathrm{solution}\:\mathrm{proves}\:\mathrm{there}\:\mathrm{are}\:\mathrm{4}\:\mathrm{real}\:\mathrm{intersections}. \\ $$$$\mathrm{It}'\mathrm{s}\:\mathrm{obviously}\:\mathrm{a}\:\mathrm{problem}\:\mathrm{of}\:\mathrm{the}\:\mathrm{approximation}. \\ $$$$\mathrm{An}\:\mathrm{imaginary}\:\mathrm{part}\:\mathrm{of}\:\approx.\mathrm{0000000000000001i} \\ $$$$\mathrm{is}\:\mathrm{strange}.\:\mathrm{But}\:\mathrm{as}\:\mathrm{I}\:\mathrm{wrote}\:\mathrm{before},\:\mathrm{your} \\ $$$$\mathrm{picture}\:\mathrm{also}\:\mathrm{shows}\:\mathrm{4}\:\mathrm{real}\:\mathrm{solutions}.\:\mathrm{Do}\:\mathrm{you} \\ $$$$\mathrm{trust}\:\mathrm{more}\:\mathrm{in}\:\mathrm{an}\:\mathrm{algorithm}? \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com