
Question Number 195291 by Matica last updated on 29/Jul/23
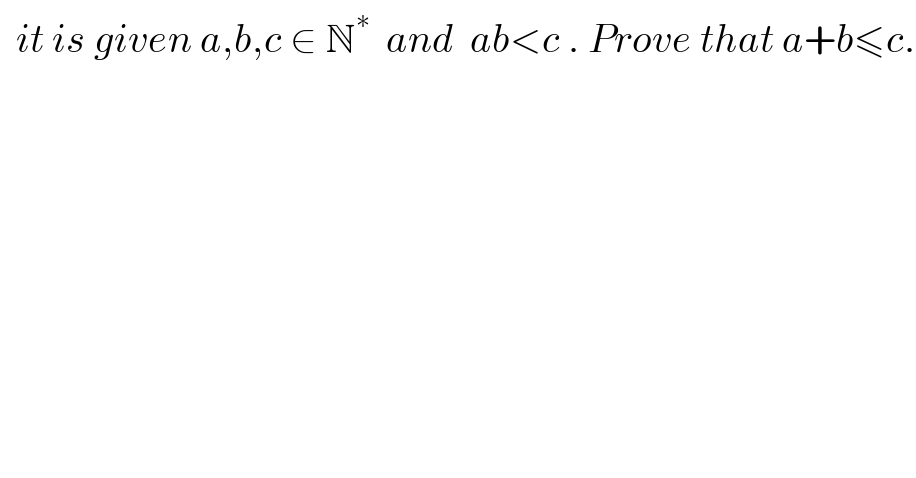
$$\:\:{it}\:{is}\:{given}\:{a},{b},{c}\:\in\:\mathbb{N}^{\ast} \:\:{and}\:\:{ab}<{c}\:.\:{Prove}\:{that}\:{a}+{b}\leqslant{c}. \\ $$
Answered by Frix last updated on 29/Jul/23
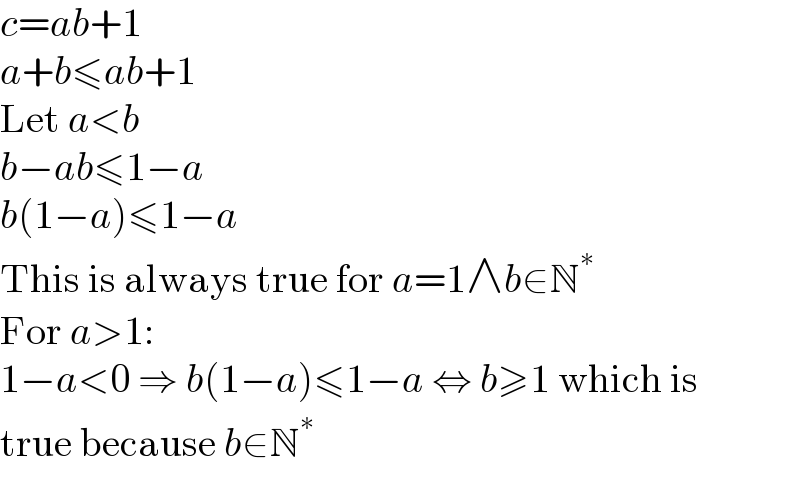
$${c}={ab}+\mathrm{1} \\ $$$${a}+{b}\leqslant{ab}+\mathrm{1} \\ $$$$\mathrm{Let}\:{a}<{b} \\ $$$${b}−{ab}\leqslant\mathrm{1}−{a} \\ $$$${b}\left(\mathrm{1}−{a}\right)\leqslant\mathrm{1}−{a} \\ $$$$\mathrm{This}\:\mathrm{is}\:\mathrm{always}\:\mathrm{true}\:\mathrm{for}\:{a}=\mathrm{1}\wedge{b}\in\mathbb{N}^{\ast} \\ $$$$\mathrm{For}\:{a}>\mathrm{1}: \\ $$$$\mathrm{1}−{a}<\mathrm{0}\:\Rightarrow\:{b}\left(\mathrm{1}−{a}\right)\leqslant\mathrm{1}−{a}\:\Leftrightarrow\:{b}\geqslant\mathrm{1}\:\mathrm{which}\:\mathrm{is} \\ $$$$\mathrm{true}\:\mathrm{because}\:{b}\in\mathbb{N}^{\ast} \\ $$
