
Question Number 195253 by Spillover last updated on 28/Jul/23
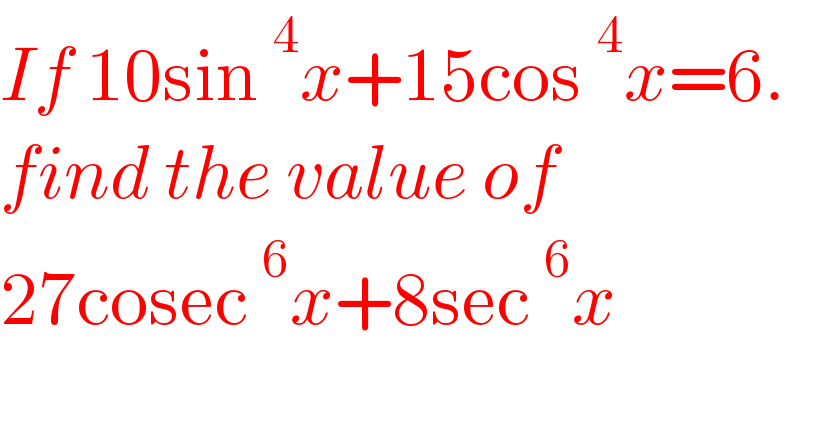
$${If}\:\mathrm{10sin}\:^{\mathrm{4}} {x}+\mathrm{15cos}\:^{\mathrm{4}} {x}=\mathrm{6}. \\ $$$${find}\:{the}\:{value}\:{of} \\ $$$$\mathrm{27cosec}\:^{\mathrm{6}} {x}+\mathrm{8sec}\:^{\mathrm{6}} {x} \\ $$$$ \\ $$
Commented by Frix last updated on 28/Jul/23

$$\mathrm{250} \\ $$
Answered by BaliramKumar last updated on 28/Jul/23
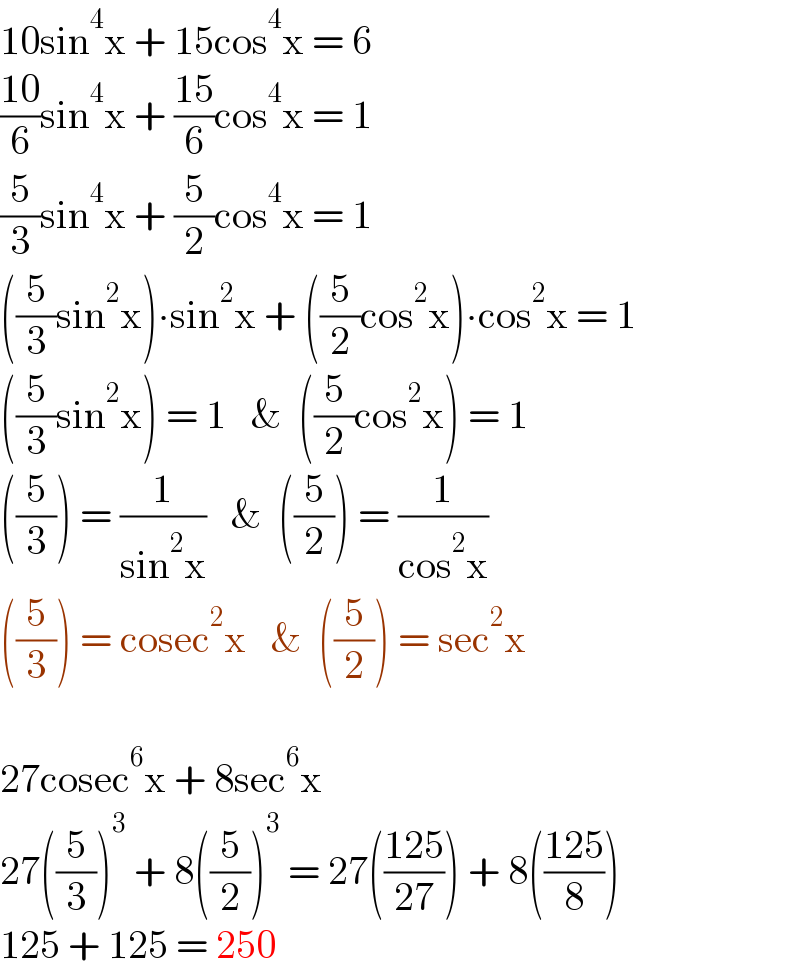
$$\mathrm{10sin}^{\mathrm{4}} \mathrm{x}\:+\:\mathrm{15cos}^{\mathrm{4}} \mathrm{x}\:=\:\mathrm{6} \\ $$$$\frac{\mathrm{10}}{\mathrm{6}}\mathrm{sin}^{\mathrm{4}} \mathrm{x}\:+\:\frac{\mathrm{15}}{\mathrm{6}}\mathrm{cos}^{\mathrm{4}} \mathrm{x}\:=\:\mathrm{1} \\ $$$$\frac{\mathrm{5}}{\mathrm{3}}\mathrm{sin}^{\mathrm{4}} \mathrm{x}\:+\:\frac{\mathrm{5}}{\mathrm{2}}\mathrm{cos}^{\mathrm{4}} \mathrm{x}\:=\:\mathrm{1} \\ $$$$\left(\frac{\mathrm{5}}{\mathrm{3}}\mathrm{sin}^{\mathrm{2}} \mathrm{x}\right)\centerdot\mathrm{sin}^{\mathrm{2}} \mathrm{x}\:+\:\left(\frac{\mathrm{5}}{\mathrm{2}}\mathrm{cos}^{\mathrm{2}} \mathrm{x}\right)\centerdot\mathrm{cos}^{\mathrm{2}} \mathrm{x}\:=\:\mathrm{1} \\ $$$$\left(\frac{\mathrm{5}}{\mathrm{3}}\mathrm{sin}^{\mathrm{2}} \mathrm{x}\right)\:=\:\mathrm{1}\:\:\:\&\:\:\left(\frac{\mathrm{5}}{\mathrm{2}}\mathrm{cos}^{\mathrm{2}} \mathrm{x}\right)\:=\:\mathrm{1} \\ $$$$\left(\frac{\mathrm{5}}{\mathrm{3}}\right)\:=\:\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{2}} \mathrm{x}}\:\:\:\&\:\:\left(\frac{\mathrm{5}}{\mathrm{2}}\right)\:=\:\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} \mathrm{x}} \\ $$$$\left(\frac{\mathrm{5}}{\mathrm{3}}\right)\:=\:\mathrm{cosec}^{\mathrm{2}} \mathrm{x}\:\:\:\&\:\:\left(\frac{\mathrm{5}}{\mathrm{2}}\right)\:=\:\mathrm{sec}^{\mathrm{2}} \mathrm{x} \\ $$$$ \\ $$$$\mathrm{27cosec}^{\mathrm{6}} \mathrm{x}\:+\:\mathrm{8sec}^{\mathrm{6}} \mathrm{x} \\ $$$$\mathrm{27}\left(\frac{\mathrm{5}}{\mathrm{3}}\right)^{\mathrm{3}} \:+\:\mathrm{8}\left(\frac{\mathrm{5}}{\mathrm{2}}\right)^{\mathrm{3}} \:=\:\mathrm{27}\left(\frac{\mathrm{125}}{\mathrm{27}}\right)\:+\:\mathrm{8}\left(\frac{\mathrm{125}}{\mathrm{8}}\right) \\ $$$$\mathrm{125}\:+\:\mathrm{125}\:=\:\mathrm{250} \\ $$
Commented by Spillover last updated on 03/Aug/23

$${thank}\:{you} \\ $$
Answered by Spillover last updated on 02/Aug/23
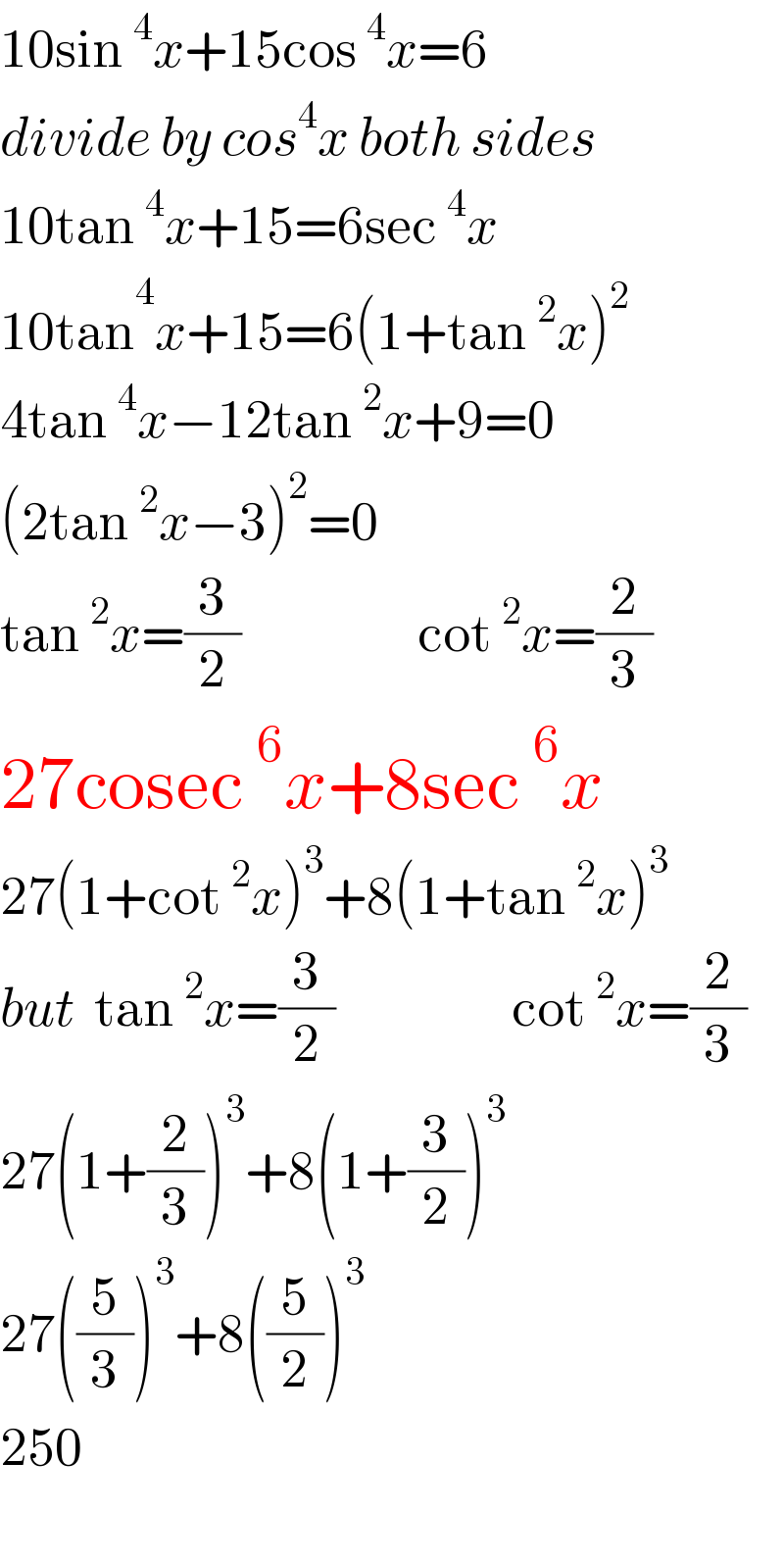
$$\mathrm{10sin}\:^{\mathrm{4}} {x}+\mathrm{15cos}\:^{\mathrm{4}} {x}=\mathrm{6} \\ $$$${divide}\:{by}\:{cos}^{\mathrm{4}} {x}\:{both}\:{sides} \\ $$$$\mathrm{10tan}\:^{\mathrm{4}} {x}+\mathrm{15}=\mathrm{6sec}\:^{\mathrm{4}} {x} \\ $$$$\mathrm{10tan}\overset{\mathrm{4}} {\:}{x}+\mathrm{15}=\mathrm{6}\left(\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} {x}\right)^{\mathrm{2}} \\ $$$$\mathrm{4tan}\:^{\mathrm{4}} {x}−\mathrm{12tan}\:^{\mathrm{2}} {x}+\mathrm{9}=\mathrm{0} \\ $$$$\left(\mathrm{2tan}\:^{\mathrm{2}} {x}−\mathrm{3}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{tan}\:^{\mathrm{2}} {x}=\frac{\mathrm{3}}{\mathrm{2}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{cot}\:^{\mathrm{2}} {x}=\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\mathrm{27cosec}\:^{\mathrm{6}} {x}+\mathrm{8sec}\:^{\mathrm{6}} {x} \\ $$$$\mathrm{27}\left(\mathrm{1}+\mathrm{cot}\:^{\mathrm{2}} {x}\right)^{\mathrm{3}} +\mathrm{8}\left(\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} {x}\right)^{\mathrm{3}} \\ $$$${but}\:\:\mathrm{tan}\:^{\mathrm{2}} {x}=\frac{\mathrm{3}}{\mathrm{2}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{cot}\:^{\mathrm{2}} {x}=\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\mathrm{27}\left(\mathrm{1}+\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{3}} +\mathrm{8}\left(\mathrm{1}+\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{3}} \\ $$$$\mathrm{27}\left(\frac{\mathrm{5}}{\mathrm{3}}\right)^{\mathrm{3}} +\mathrm{8}\left(\frac{\mathrm{5}}{\mathrm{2}}\right)^{\mathrm{3}} \\ $$$$\mathrm{250} \\ $$$$ \\ $$
