
Previous in Matrices and Determinants Next in Matrices and Determinants
Question Number 195203 by Erico last updated on 27/Jul/23
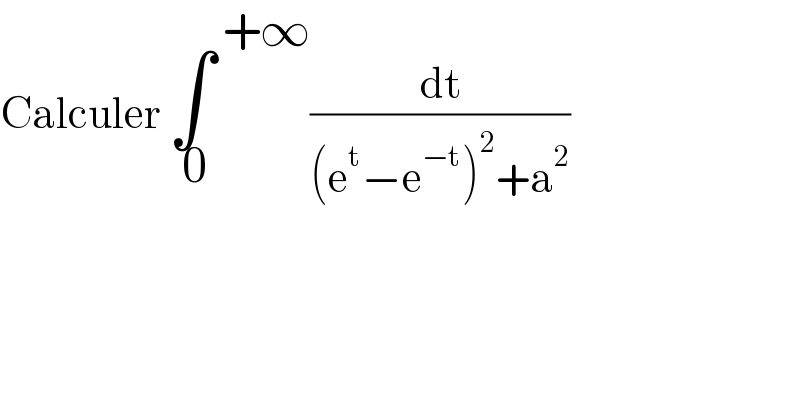
$$\mathrm{Calculer}\:\underset{\:\mathrm{0}} {\int}^{\:+\infty} \frac{\mathrm{dt}}{\left(\mathrm{e}^{\mathrm{t}} −\mathrm{e}^{−\mathrm{t}} \right)^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} } \\ $$
Answered by Frix last updated on 27/Jul/23
![∫_0 ^∞ (dt/((e^t −e^(−t) )^2 +a^2 )) =^([u=e^(2t) ]) =(1/2)∫_1 ^∞ (du/(u^2 +(a^2 −2)u+1))= =(1/(2a(√(a^2 −4))))[ln ∣((2u+a^2 −2+a(√(a^2 −4)))/(2u+a^2 −2−a(√(a^2 −4))))∣]_1 ^∞ = =(1/(2a(√(a^2 −4))))ln ∣((a−(√(a^2 −4)))/(a+(√(a^2 −4))))∣](Q195214.png)
$$\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{{dt}}{\left(\mathrm{e}^{{t}} −\mathrm{e}^{−{t}} \right)^{\mathrm{2}} +{a}^{\mathrm{2}} }\:\overset{\left[{u}=\mathrm{e}^{\mathrm{2}{t}} \right]} {=} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\underset{\mathrm{1}} {\overset{\infty} {\int}}\frac{{du}}{{u}^{\mathrm{2}} +\left({a}^{\mathrm{2}} −\mathrm{2}\right){u}+\mathrm{1}}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{a}\sqrt{{a}^{\mathrm{2}} −\mathrm{4}}}\left[\mathrm{ln}\:\mid\frac{\mathrm{2}{u}+{a}^{\mathrm{2}} −\mathrm{2}+{a}\sqrt{{a}^{\mathrm{2}} −\mathrm{4}}}{\mathrm{2}{u}+{a}^{\mathrm{2}} −\mathrm{2}−{a}\sqrt{{a}^{\mathrm{2}} −\mathrm{4}}}\mid\right]_{\mathrm{1}} ^{\infty} = \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{a}\sqrt{{a}^{\mathrm{2}} −\mathrm{4}}}\mathrm{ln}\:\mid\frac{{a}−\sqrt{{a}^{\mathrm{2}} −\mathrm{4}}}{{a}+\sqrt{{a}^{\mathrm{2}} −\mathrm{4}}}\mid \\ $$
