
Question Number 195180 by mustafazaheen last updated on 26/Jul/23
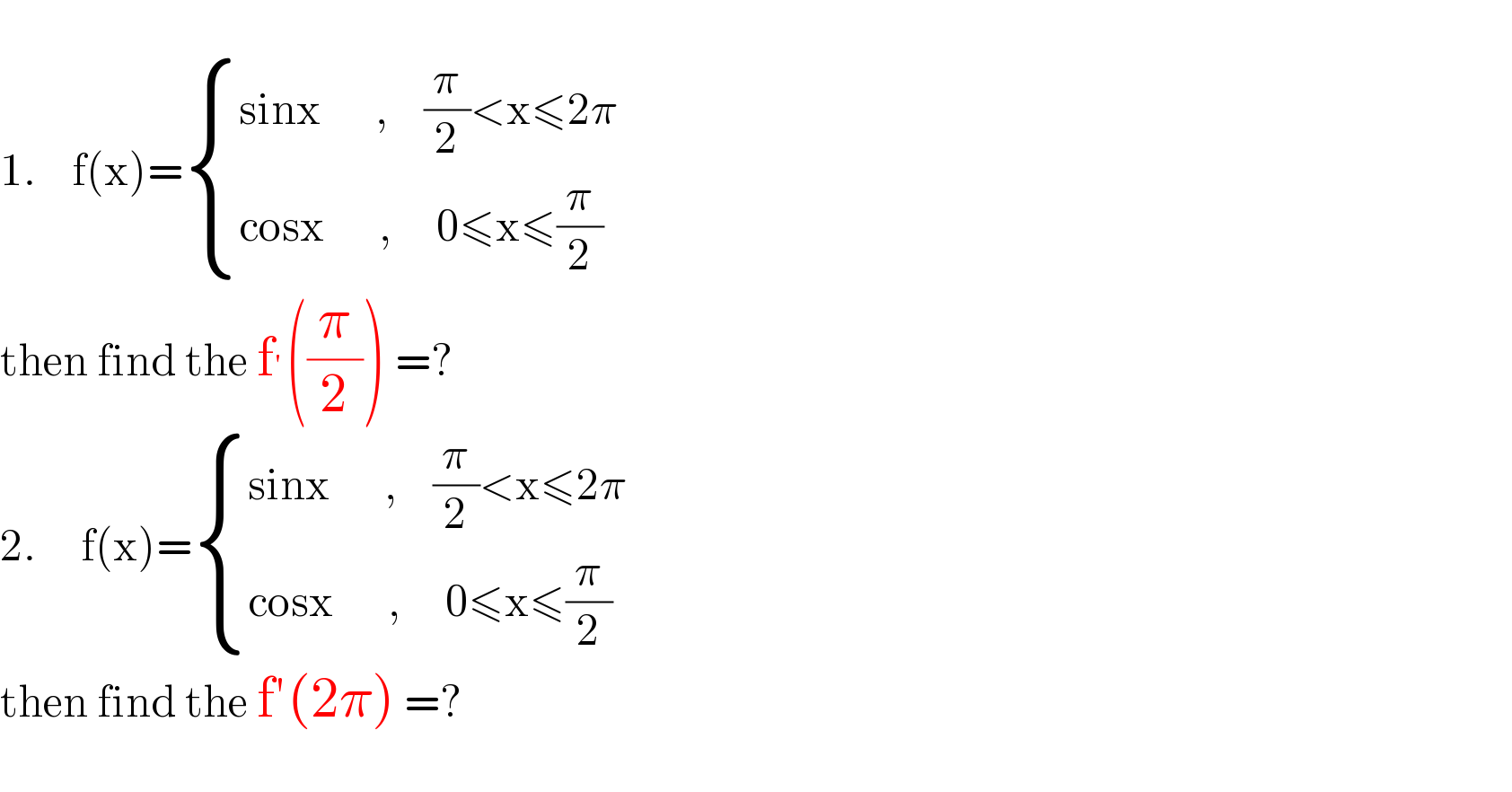
$$ \\ $$$$\mathrm{1}.\:\:\:\:\mathrm{f}\left(\mathrm{x}\right)=\begin{cases}{\mathrm{sinx}\:\:\:\:\:\:,\:\:\:\:\frac{\pi}{\mathrm{2}}<\mathrm{x}\leqslant\mathrm{2}\pi}\\{\mathrm{cosx}\:\:\:\:\:\:,\:\:\:\:\:\mathrm{0}\leqslant\mathrm{x}\leqslant\frac{\pi}{\mathrm{2}}}\end{cases} \\ $$$$\mathrm{then}\:\mathrm{find}\:\mathrm{the}\:\mathrm{f}^{'} \left(\frac{\pi}{\mathrm{2}}\right)\:=? \\ $$$$\mathrm{2}.\:\:\:\:\:\mathrm{f}\left(\mathrm{x}\right)=\begin{cases}{\mathrm{sinx}\:\:\:\:\:\:,\:\:\:\:\frac{\pi}{\mathrm{2}}<\mathrm{x}\leqslant\mathrm{2}\pi}\\{\mathrm{cosx}\:\:\:\:\:\:,\:\:\:\:\:\mathrm{0}\leqslant\mathrm{x}\leqslant\frac{\pi}{\mathrm{2}}}\end{cases} \\ $$$$\mathrm{then}\:\mathrm{find}\:\mathrm{the}\:\mathrm{f}'\left(\mathrm{2}\pi\right)\:=? \\ $$$$ \\ $$
Answered by mathlove last updated on 26/Jul/23
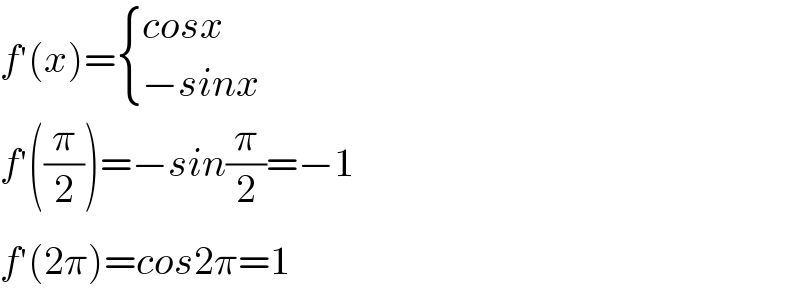
$${f}^{'} \left({x}\right)=\begin{cases}{{cosx}}\\{−{sinx}}\end{cases} \\ $$$${f}^{'} \left(\frac{\pi}{\mathrm{2}}\right)=−{sin}\frac{\pi}{\mathrm{2}}=−\mathrm{1} \\ $$$${f}^{'} \left(\mathrm{2}\pi\right)={cos}\mathrm{2}\pi=\mathrm{1} \\ $$
Commented by MM42 last updated on 26/Jul/23

$${The}\:{function}\:{is}\:{not}\:{continuouse}\:\:{in} \\ $$$${x}=\frac{\pi}{\mathrm{2}}.{therefore}\:{it}\:{is}\:{not}\:{differentiable}\:{in}\:{x}=\frac{\pi}{\mathrm{2}} \\ $$
