
Question Number 195178 by Shlock last updated on 26/Jul/23
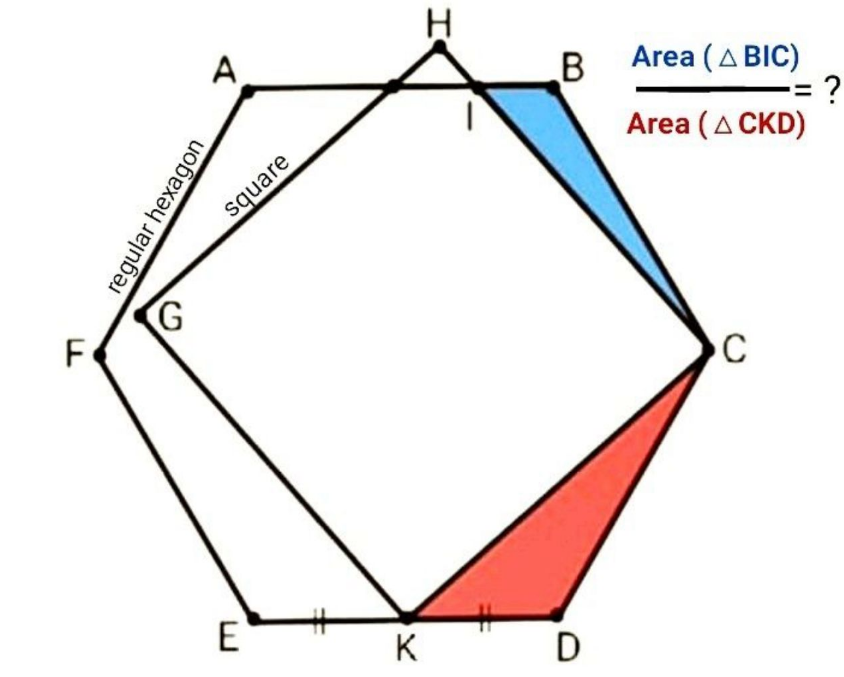
Answered by mr W last updated on 26/Jul/23
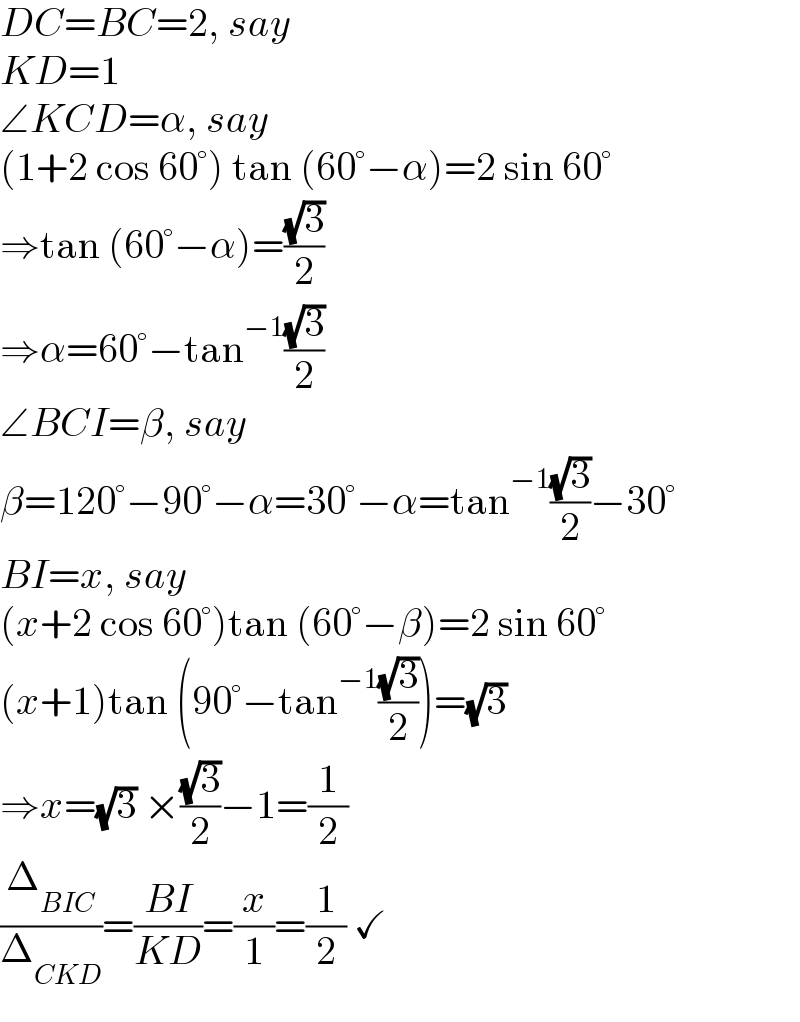
$${DC}={BC}=\mathrm{2},\:{say} \\ $$$${KD}=\mathrm{1} \\ $$$$\angle{KCD}=\alpha,\:{say} \\ $$$$\left(\mathrm{1}+\mathrm{2}\:\mathrm{cos}\:\mathrm{60}°\right)\:\mathrm{tan}\:\left(\mathrm{60}°−\alpha\right)=\mathrm{2}\:\mathrm{sin}\:\mathrm{60}° \\ $$$$\Rightarrow\mathrm{tan}\:\left(\mathrm{60}°−\alpha\right)=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\Rightarrow\alpha=\mathrm{60}°−\mathrm{tan}^{−\mathrm{1}} \frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\angle{BCI}=\beta,\:{say} \\ $$$$\beta=\mathrm{120}°−\mathrm{90}°−\alpha=\mathrm{30}°−\alpha=\mathrm{tan}^{−\mathrm{1}} \frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\mathrm{30}° \\ $$$${BI}={x},\:{say} \\ $$$$\left({x}+\mathrm{2}\:\mathrm{cos}\:\mathrm{60}°\right)\mathrm{tan}\:\left(\mathrm{60}°−\beta\right)=\mathrm{2}\:\mathrm{sin}\:\mathrm{60}° \\ $$$$\left({x}+\mathrm{1}\right)\mathrm{tan}\:\left(\mathrm{90}°−\mathrm{tan}^{−\mathrm{1}} \frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)=\sqrt{\mathrm{3}} \\ $$$$\Rightarrow{x}=\sqrt{\mathrm{3}}\:×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\mathrm{1}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\frac{\Delta_{{BIC}} }{\Delta_{{CKD}} }=\frac{{BI}}{{KD}}=\frac{{x}}{\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{2}}\:\checkmark \\ $$
Commented by Shlock last updated on 26/Jul/23
Nice work, Prof!
Answered by mr W last updated on 27/Jul/23

Commented by mr W last updated on 27/Jul/23
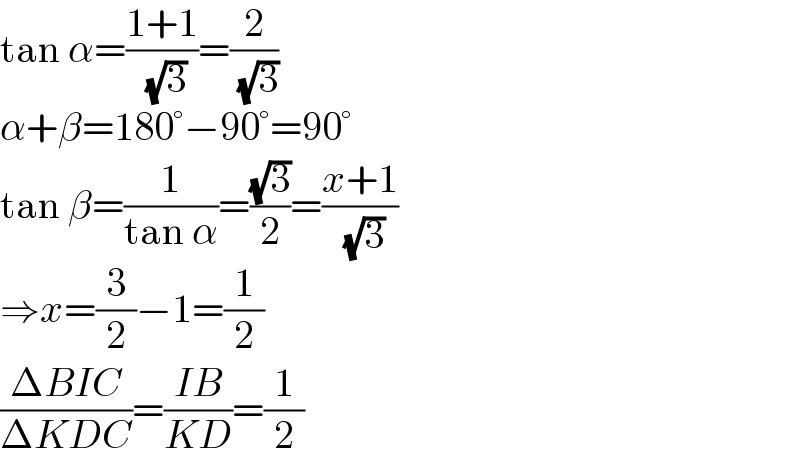
$$\mathrm{tan}\:\alpha=\frac{\mathrm{1}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}} \\ $$$$\alpha+\beta=\mathrm{180}°−\mathrm{90}°=\mathrm{90}° \\ $$$$\mathrm{tan}\:\beta=\frac{\mathrm{1}}{\mathrm{tan}\:\alpha}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}=\frac{{x}+\mathrm{1}}{\:\sqrt{\mathrm{3}}} \\ $$$$\Rightarrow{x}=\frac{\mathrm{3}}{\mathrm{2}}−\mathrm{1}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\frac{\Delta{BIC}}{\Delta{KDC}}=\frac{{IB}}{{KD}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
