
Question Number 195170 by mathlove last updated on 25/Jul/23
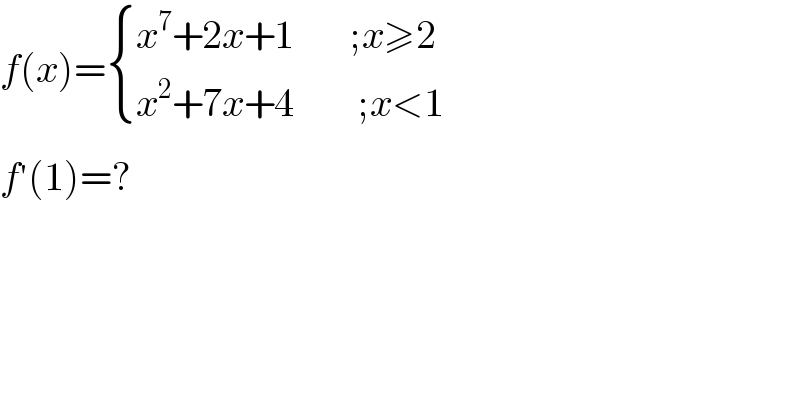
$${f}\left({x}\right)=\begin{cases}{{x}^{\mathrm{7}} +\mathrm{2}{x}+\mathrm{1}\:\:\:\:\:\:\:;{x}\geqslant\mathrm{2}}\\{{x}^{\mathrm{2}} +\mathrm{7}{x}+\mathrm{4}\:\:\:\:\:\:\:\:;{x}<\mathrm{1}}\end{cases} \\ $$$${f}^{'} \left(\mathrm{1}\right)=? \\ $$
Answered by MM42 last updated on 25/Jul/23
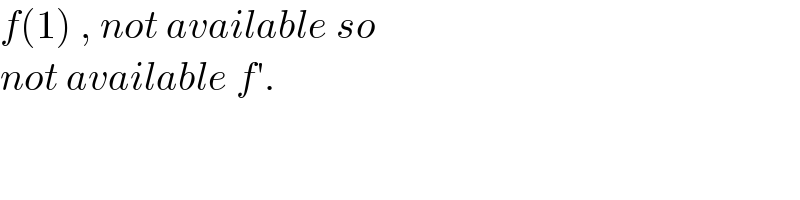
$${f}\left(\mathrm{1}\right)\:,\:{not}\:{available}\:{so} \\ $$$${not}\:{available}\:{f}'. \\ $$
Answered by dimentri last updated on 25/Jul/23
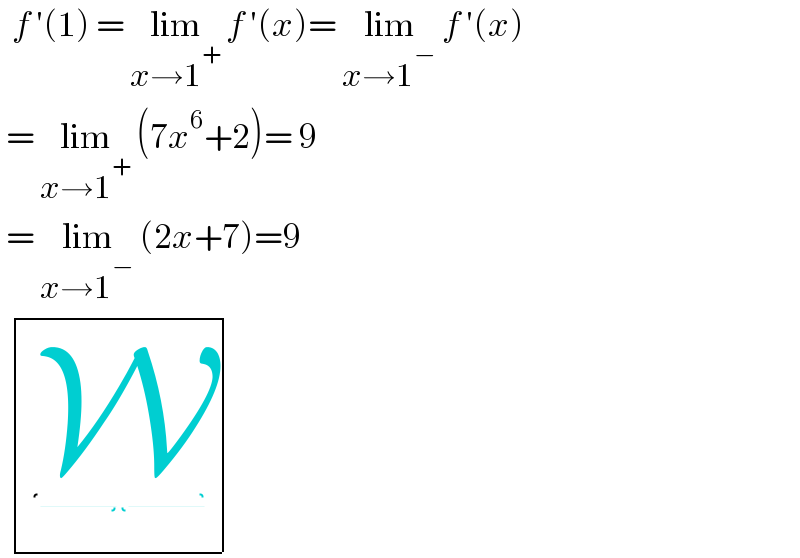
$$\:\:{f}\:'\left(\mathrm{1}\right)\:=\:\underset{{x}\rightarrow\mathrm{1}^{+} } {\mathrm{lim}}\:{f}\:'\left({x}\right)=\:\underset{{x}\rightarrow\mathrm{1}^{−} } {\mathrm{lim}}\:{f}\:'\left({x}\right) \\ $$$$\:=\:\underset{{x}\rightarrow\mathrm{1}^{+} } {\mathrm{lim}}\:\left(\mathrm{7}{x}^{\mathrm{6}} +\mathrm{2}\right)=\:\mathrm{9} \\ $$$$\:=\:\underset{{x}\rightarrow\mathrm{1}^{−} } {\mathrm{lim}}\:\left(\mathrm{2}{x}+\mathrm{7}\right)=\mathrm{9} \\ $$$$\:\begin{array}{|c|}{ }\\\hline\end{array} \\ $$
Commented by MM42 last updated on 25/Jul/23
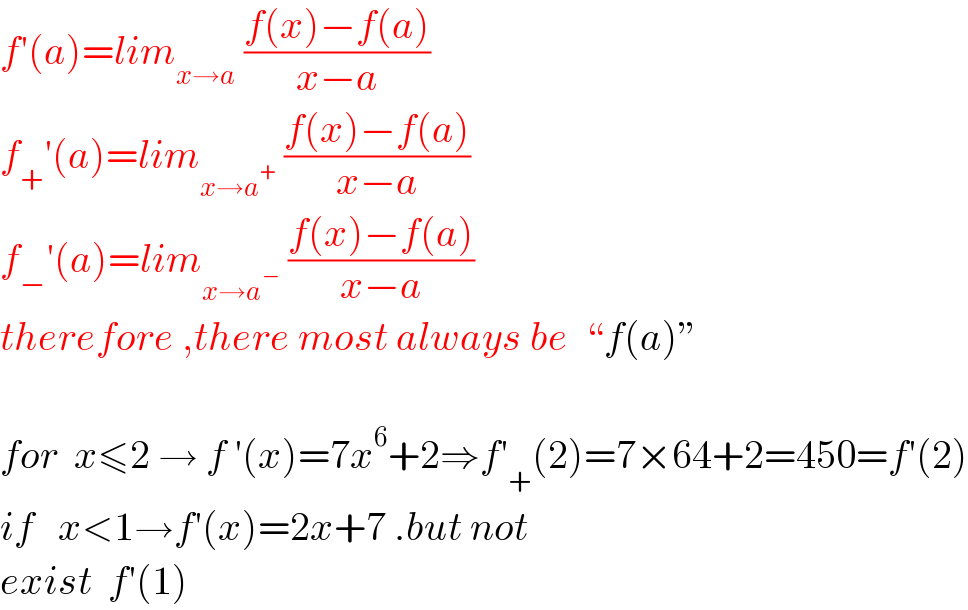
$${f}'\left({a}\right)={lim}_{{x}\rightarrow{a}} \:\frac{{f}\left({x}\right)−{f}\left({a}\right)}{{x}−{a}} \\ $$$${f}_{+} '\left({a}\right)={lim}_{{x}\rightarrow{a}^{+} } \:\frac{{f}\left({x}\right)−{f}\left({a}\right)}{{x}−{a}} \\ $$$${f}_{−} '\left({a}\right)={lim}_{{x}\rightarrow{a}^{−} } \:\frac{{f}\left({x}\right)−{f}\left({a}\right)}{{x}−{a}} \\ $$$${therefore}\:,{there}\:{most}\:{always}\:{be}\:\:``{f}\left({a}\right)'' \\ $$$$ \\ $$$${for}\:\:{x}\leqslant\mathrm{2}\:\rightarrow\:{f}\:'\left({x}\right)=\mathrm{7}{x}^{\mathrm{6}} +\mathrm{2}\Rightarrow{f}'_{+} \left(\mathrm{2}\right)=\mathrm{7}×\mathrm{64}+\mathrm{2}=\mathrm{450}={f}'\left(\mathrm{2}\right) \\ $$$${if}\:\:\:{x}<\mathrm{1}\rightarrow{f}'\left({x}\right)=\mathrm{2}{x}+\mathrm{7}\:.{but}\:{not}\: \\ $$$${exist}\:\:{f}'\left(\mathrm{1}\right) \\ $$
Commented by mathlove last updated on 26/Jul/23
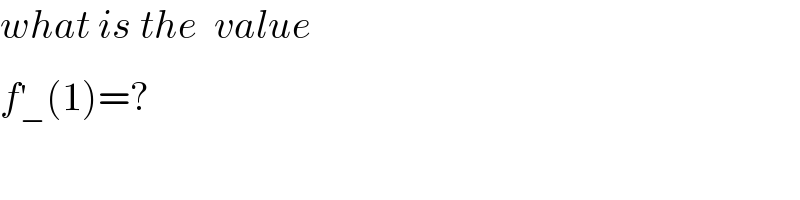
$${what}\:{is}\:{the}\:\:{value} \\ $$$${f}_{−} ^{'} \left(\mathrm{1}\right)=?\:\:\:\: \\ $$
Commented by MM42 last updated on 26/Jul/23

$${not}\:{exist}.{because}\:{not}\:{exist}\:\:{f}\left(\mathrm{1}\right) \\ $$
