
Question Number 195065 by alcohol last updated on 23/Jul/23

Answered by Rasheed.Sindhi last updated on 23/Jul/23

$${Let}\:{a}−{d},{a},{a}+{d}\:{are}\:{required}\:{numbers} \\ $$$$\left({a}−{d}\right)+{a}+\left({a}+{d}\right)=\mathrm{21} \\ $$$$\mathrm{3}{a}=\mathrm{21}\Rightarrow{a}=\mathrm{7} \\ $$$$\therefore\:\:\mathrm{7}−{d},\mathrm{7},\mathrm{7}+{d}\:{are}\:{required}\:{numbers} \\ $$$${Now}\:{by}\:{given}:\: \\ $$$$\left(\mathrm{7}−{d}\right)+\mathrm{2},\mathrm{7}+\mathrm{3},\left(\mathrm{7}+{d}\right)+\mathrm{9}\:{are}\:{inGP} \\ $$$$\mathrm{9}−{d},\mathrm{10},\mathrm{16}+{d}\:{are}\:{inGP} \\ $$$$\Rightarrow\frac{\mathrm{10}}{\mathrm{9}−{d}}=\frac{\mathrm{16}+{d}}{\mathrm{10}} \\ $$$$\:\:\:\:\mathrm{144}−\mathrm{16}{d}+\mathrm{9}{d}−{d}^{\mathrm{2}} =\mathrm{100} \\ $$$$\:\:\:\:\:{d}^{\mathrm{2}} +\mathrm{7}{d}−\mathrm{44}=\mathrm{0} \\ $$$$\:\:\:\:\:\left({d}+\mathrm{11}\right)\left({d}−\mathrm{4}\right)=\mathrm{0} \\ $$$$\:\:\:\:\:{d}=−\mathrm{11},\mathrm{4} \\ $$$$\bullet{d}=−\mathrm{11}: \\ $$$$\mathrm{7}−\left(−\mathrm{11}\right),\mathrm{7},\mathrm{7}+\left(−\mathrm{11}\right) \\ $$$$\mathrm{18},\mathrm{7},−\mathrm{4}\:\:\left({Rejected}\:{because}\:−\mathrm{4}\:{is}\:{not}\:+{ve}\right) \\ $$$$\bullet{d}=\mathrm{4}: \\ $$$$\mathrm{7}−\mathrm{4},\mathrm{7},\mathrm{7}+\mathrm{4} \\ $$$$\mathrm{3},\mathrm{7},\mathrm{11}\checkmark \\ $$
Answered by Rasheed.Sindhi last updated on 23/Jul/23
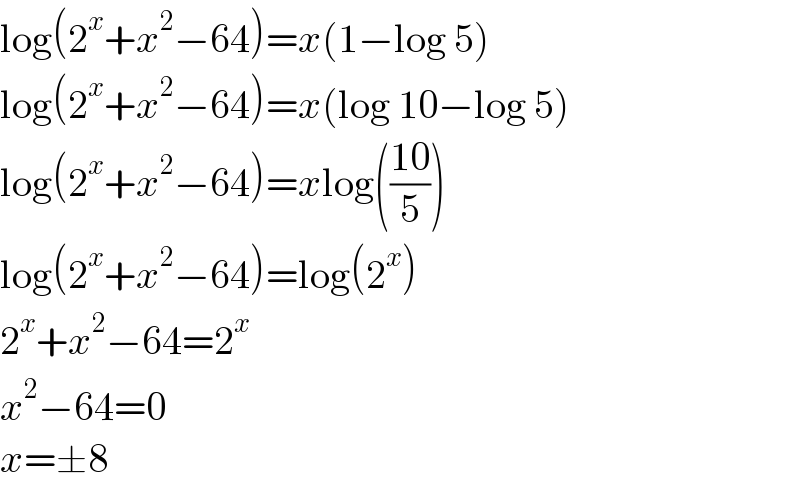
$$\mathrm{log}\left(\mathrm{2}^{{x}} +{x}^{\mathrm{2}} −\mathrm{64}\right)={x}\left(\mathrm{1}−\mathrm{log}\:\mathrm{5}\right)\: \\ $$$$\mathrm{log}\left(\mathrm{2}^{{x}} +{x}^{\mathrm{2}} −\mathrm{64}\right)={x}\left(\mathrm{log}\:\mathrm{10}−\mathrm{log}\:\mathrm{5}\right)\: \\ $$$$\mathrm{log}\left(\mathrm{2}^{{x}} +{x}^{\mathrm{2}} −\mathrm{64}\right)={x}\mathrm{log}\left(\frac{\mathrm{10}}{\mathrm{5}}\right)\: \\ $$$$\mathrm{log}\left(\mathrm{2}^{{x}} +{x}^{\mathrm{2}} −\mathrm{64}\right)=\mathrm{log}\left(\mathrm{2}^{{x}} \right)\: \\ $$$$\mathrm{2}^{{x}} +{x}^{\mathrm{2}} −\mathrm{64}=\mathrm{2}^{{x}} \: \\ $$$${x}^{\mathrm{2}} −\mathrm{64}=\mathrm{0} \\ $$$${x}=\pm\mathrm{8} \\ $$
