
Question Number 19506 by Tinkutara last updated on 12/Aug/17
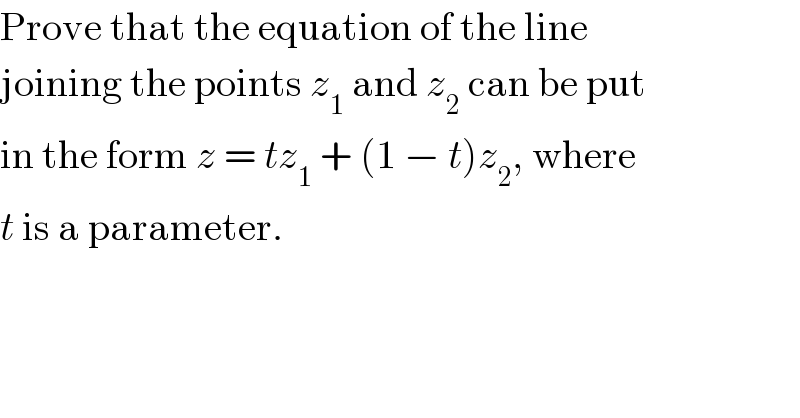
$$\mathrm{Prove}\:\mathrm{that}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{of}\:\mathrm{the}\:\mathrm{line} \\ $$$$\mathrm{joining}\:\mathrm{the}\:\mathrm{points}\:{z}_{\mathrm{1}} \:\mathrm{and}\:{z}_{\mathrm{2}} \:\mathrm{can}\:\mathrm{be}\:\mathrm{put} \\ $$$$\mathrm{in}\:\mathrm{the}\:\mathrm{form}\:{z}\:=\:{tz}_{\mathrm{1}} \:+\:\left(\mathrm{1}\:−\:{t}\right){z}_{\mathrm{2}} ,\:\mathrm{where} \\ $$$${t}\:\mathrm{is}\:\mathrm{a}\:\mathrm{parameter}. \\ $$
Answered by ajfour last updated on 12/Aug/17
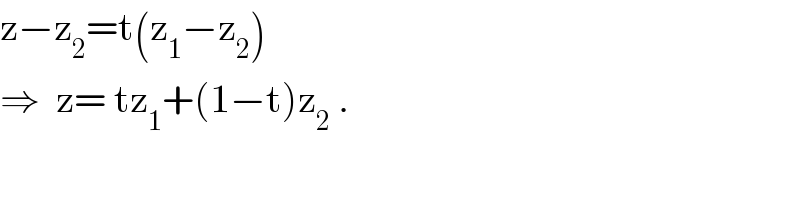
$$\mathrm{z}−\mathrm{z}_{\mathrm{2}} =\mathrm{t}\left(\mathrm{z}_{\mathrm{1}} −\mathrm{z}_{\mathrm{2}} \right) \\ $$$$\Rightarrow\:\:\mathrm{z}=\:\mathrm{tz}_{\mathrm{1}} +\left(\mathrm{1}−\mathrm{t}\right)\mathrm{z}_{\mathrm{2}} \:. \\ $$
Commented by Tinkutara last updated on 12/Aug/17
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$
Commented by ajfour last updated on 12/Aug/17
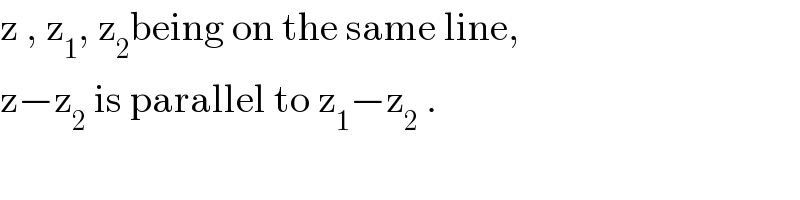
$$\mathrm{z}\:,\:\mathrm{z}_{\mathrm{1}} ,\:\mathrm{z}_{\mathrm{2}} \mathrm{being}\:\mathrm{on}\:\mathrm{the}\:\mathrm{same}\:\mathrm{line}, \\ $$$$\mathrm{z}−\mathrm{z}_{\mathrm{2}} \:\mathrm{is}\:\mathrm{parallel}\:\mathrm{to}\:\mathrm{z}_{\mathrm{1}} −\mathrm{z}_{\mathrm{2}} \:. \\ $$
