
Question Number 195033 by mathlove last updated on 22/Jul/23
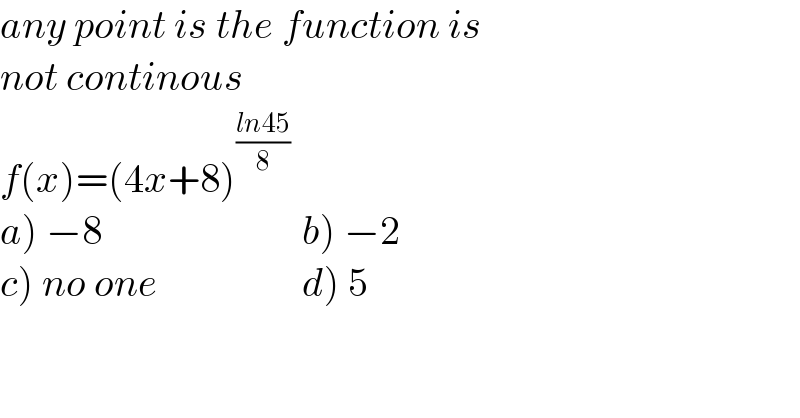
$${any}\:{point}\:{is}\:{the}\:{function}\:{is} \\ $$$${not}\:{continous} \\ $$$${f}\left({x}\right)=\left(\mathrm{4}{x}+\mathrm{8}\right)^{\frac{{ln}\mathrm{45}}{\mathrm{8}}} \\ $$$$\left.{a}\left.\right)\:−\mathrm{8}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{b}\right)\:−\mathrm{2} \\ $$$$\left.{c}\left.\right)\:{no}\:{one}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{d}\right)\:\mathrm{5} \\ $$
Answered by alephzero last updated on 22/Jul/23
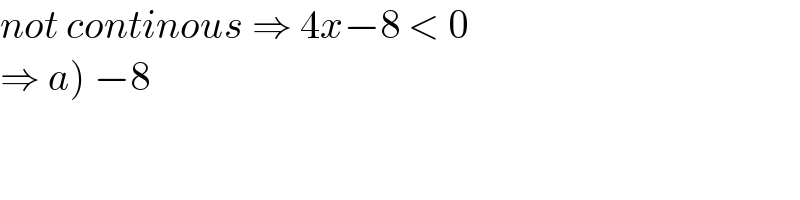
$${not}\:{continous}\:\Rightarrow\:\mathrm{4}{x}−\mathrm{8}\:<\:\mathrm{0} \\ $$$$\left.\Rightarrow\:{a}\right)\:−\mathrm{8} \\ $$
Commented by mathlove last updated on 22/Jul/23
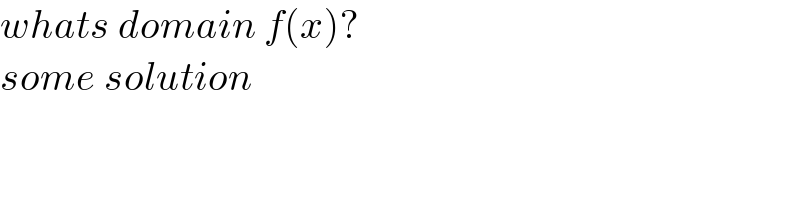
$${whats}\:{domain}\:{f}\left({x}\right)? \\ $$$${some}\:{solution} \\ $$
Commented by alephzero last updated on 22/Jul/23
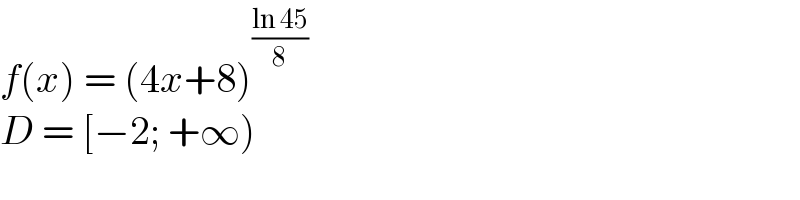
$${f}\left({x}\right)\:=\:\left(\mathrm{4}{x}+\mathrm{8}\right)^{\frac{\mathrm{ln}\:\mathrm{45}}{\mathrm{8}}} \\ $$$${D}\:=\:\left[−\mathrm{2};\:+\infty\right) \\ $$
