
Previous in Differential Equation Next in Differential Equation
Question Number 195003 by mathlove last updated on 22/Jul/23
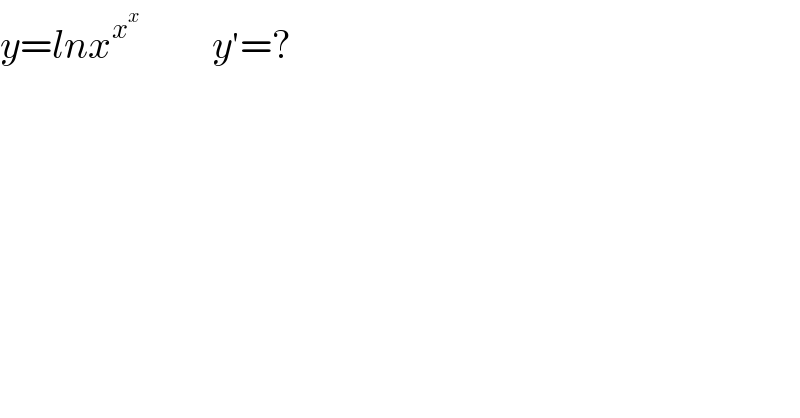
$${y}={lnx}^{{x}^{{x}} } \:\:\:\:\:\:\:\:\:{y}^{'} =? \\ $$
Answered by shunmisaki007 last updated on 22/Jul/23
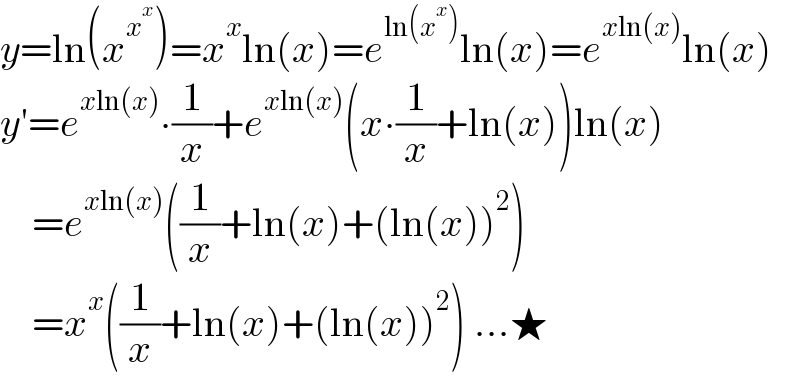
$${y}=\mathrm{ln}\left({x}^{{x}^{{x}} } \right)={x}^{{x}} \mathrm{ln}\left({x}\right)={e}^{\mathrm{ln}\left({x}^{{x}} \right)} \mathrm{ln}\left({x}\right)={e}^{{x}\mathrm{ln}\left({x}\right)} \mathrm{ln}\left({x}\right) \\ $$$${y}'={e}^{{x}\mathrm{ln}\left({x}\right)} \centerdot\frac{\mathrm{1}}{{x}}+{e}^{{x}\mathrm{ln}\left({x}\right)} \left({x}\centerdot\frac{\mathrm{1}}{{x}}+\mathrm{ln}\left({x}\right)\right)\mathrm{ln}\left({x}\right) \\ $$$$\:\:\:\:={e}^{{x}\mathrm{ln}\left({x}\right)} \left(\frac{\mathrm{1}}{{x}}+\mathrm{ln}\left({x}\right)+\left(\mathrm{ln}\left({x}\right)\right)^{\mathrm{2}} \right) \\ $$$$\:\:\:\:={x}^{{x}} \left(\frac{\mathrm{1}}{{x}}+\mathrm{ln}\left({x}\right)+\left(\mathrm{ln}\left({x}\right)\right)^{\mathrm{2}} \right)\:...\bigstar \\ $$
Commented by mathlove last updated on 22/Jul/23

$${thanks} \\ $$
