
Question Number 19499 by tawa tawa last updated on 12/Aug/17
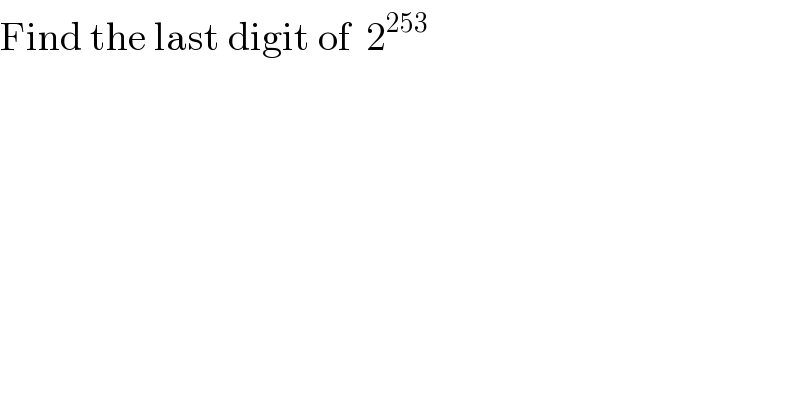
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{last}\:\mathrm{digit}\:\mathrm{of}\:\:\mathrm{2}^{\mathrm{253}} \\ $$
Answered by Tinkutara last updated on 12/Aug/17

$$\mathrm{Cyclicity}\:\mathrm{of}\:\mathrm{2}\:=\:\mathrm{4}\:\left(\mathrm{2},\:\mathrm{4},\:\mathrm{8},\:\mathrm{6}\right) \\ $$$$\mathrm{253}\:\equiv\:\mathrm{1}\:\left(\mathrm{mod}\:\mathrm{4}\right) \\ $$$$\therefore\:\mathrm{2}^{\mathrm{253}} \:\equiv\:\mathrm{2}^{\mathrm{1}} \:\equiv\:\mathrm{2} \\ $$$$\mathrm{Last}\:\mathrm{digit}\:=\:\mathrm{2} \\ $$
