Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 194942 by horsebrand11 last updated on 20/Jul/23

$$\:\:\:\:\: \\ $$

Commented by MJS_new last updated on 20/Jul/23

−2

$$−\mathrm{2} \\ $$

Commented by horsebrand11 last updated on 20/Jul/23

how ?

$$\:\mathrm{how}\:? \\ $$

Answered by MJS_new last updated on 20/Jul/23

2x=2y^3 +(1+(√5))y 2y=2x^3 +(1+(√5))x y=px 2x=2p^3 x^3 +(1+(√5))px 2px=2x^3 +(1+(√5))x x=0 ⇒ y=0 but x≠y ⇒ x≠0 2=p(2p^2 x^2 +1+(√5)) 2p=2x^2 +1+(√5) ========== x^2 =((2−(1+(√5))p)/(2p^3 ))=((2p−(1+(√5)))/2) p^4 −((1+(√5))/2)p^3 +((1+(√5))/2)p−1=0 we know that x=±y ⇒ p=±1 are solutions, now it′s easy to factorize (p−1)(p+1)(p^2 −((1+(√5))/2)+1)=0 but x≠y∧x+y≠0 p^2 −((1+(√5))/2)+1=0 p=e^(±iπ/5) y=px ⇒ (x/y)=(1/p)∧(y/x)=p ((x/y))^(2025) +((y/x))^(2025) =e^(405πi) +e^(−405πi) =e^(iπ) +e^(−iπ) = =−2

$$\mathrm{2}{x}=\mathrm{2}{y}^{\mathrm{3}} +\left(\mathrm{1}+\sqrt{\mathrm{5}}\right){y} \\ $$$$\mathrm{2}{y}=\mathrm{2}{x}^{\mathrm{3}} +\left(\mathrm{1}+\sqrt{\mathrm{5}}\right){x} \\ $$$${y}={px} \\ $$$$\mathrm{2}{x}=\mathrm{2}{p}^{\mathrm{3}} {x}^{\mathrm{3}} +\left(\mathrm{1}+\sqrt{\mathrm{5}}\right){px} \\ $$$$\mathrm{2}{px}=\mathrm{2}{x}^{\mathrm{3}} +\left(\mathrm{1}+\sqrt{\mathrm{5}}\right){x} \\ $$$${x}=\mathrm{0}\:\Rightarrow\:{y}=\mathrm{0}\:\mathrm{but}\:{x}\neq{y}\:\Rightarrow\:{x}\neq\mathrm{0} \\ $$$$\mathrm{2}={p}\left(\mathrm{2}{p}^{\mathrm{2}} {x}^{\mathrm{2}} +\mathrm{1}+\sqrt{\mathrm{5}}\right) \\ $$$$\mathrm{2}{p}=\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}+\sqrt{\mathrm{5}} \\ $$$$========== \\ $$$${x}^{\mathrm{2}} =\frac{\mathrm{2}−\left(\mathrm{1}+\sqrt{\mathrm{5}}\right){p}}{\mathrm{2}{p}^{\mathrm{3}} }=\frac{\mathrm{2}{p}−\left(\mathrm{1}+\sqrt{\mathrm{5}}\right)}{\mathrm{2}} \\ $$$${p}^{\mathrm{4}} −\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}{p}^{\mathrm{3}} +\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}{p}−\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{we}\:\mathrm{know}\:\mathrm{that}\:{x}=\pm{y}\:\Rightarrow\:{p}=\pm\mathrm{1}\:\:\mathrm{are}\:\mathrm{solutions}, \\ $$$$\mathrm{now}\:\mathrm{it}'\mathrm{s}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{factorize} \\ $$$$\left({p}−\mathrm{1}\right)\left({p}+\mathrm{1}\right)\left({p}^{\mathrm{2}} −\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\mathrm{but}\:{x}\neq{y}\wedge{x}+{y}\neq\mathrm{0} \\ $$$${p}^{\mathrm{2}} −\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}+\mathrm{1}=\mathrm{0} \\ $$$${p}=\mathrm{e}^{\pm\mathrm{i}\pi/\mathrm{5}} \\ $$$${y}={px}\:\Rightarrow\:\frac{{x}}{{y}}=\frac{\mathrm{1}}{{p}}\wedge\frac{{y}}{{x}}={p} \\ $$$$\left(\frac{{x}}{{y}}\right)^{\mathrm{2025}} +\left(\frac{{y}}{{x}}\right)^{\mathrm{2025}} =\mathrm{e}^{\mathrm{405}\pi\mathrm{i}} +\mathrm{e}^{−\mathrm{405}\pi\mathrm{i}} =\mathrm{e}^{\mathrm{i}\pi} +\mathrm{e}^{−\mathrm{i}\pi} = \\ $$$$=−\mathrm{2} \\ $$

Commented by horsebrand11 last updated on 20/Jul/23

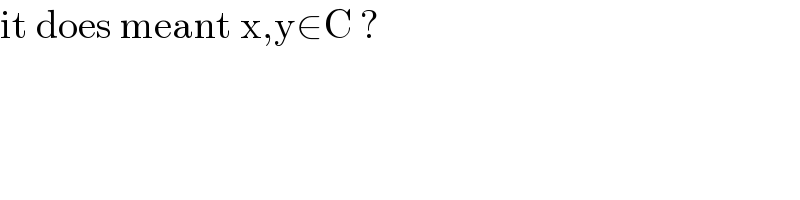
it does meant x,y∈C ?

$$\mathrm{it}\:\mathrm{does}\:\mathrm{meant}\:\mathrm{x},\mathrm{y}\in\mathrm{C}\:? \\ $$

Commented by MJS_new last updated on 20/Jul/23

yes

$$\mathrm{yes} \\ $$

Commented by horsebrand11 last updated on 20/Jul/23

thanks sir

$$\mathrm{thanks}\:\mathrm{sir} \\ $$

Commented by MJS_new last updated on 20/Jul/23

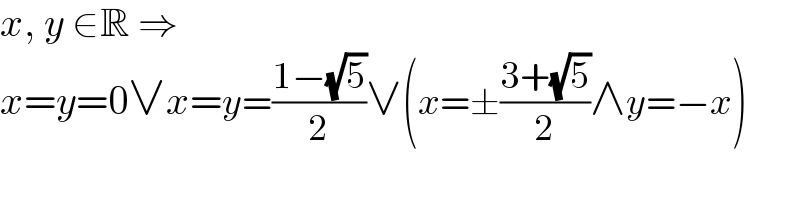
x, y ∈R ⇒ x=y=0∨x=y=((1−(√5))/2)∨(x=±((3+(√5))/2)∧y=−x)

$${x},\:{y}\:\in\mathbb{R}\:\Rightarrow\: \\ $$$${x}={y}=\mathrm{0}\vee{x}={y}=\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}\vee\left({x}=\pm\frac{\mathrm{3}+\sqrt{\mathrm{5}}}{\mathrm{2}}\wedge{y}=−{x}\right) \\ $$

Commented by MM42 last updated on 20/Jul/23

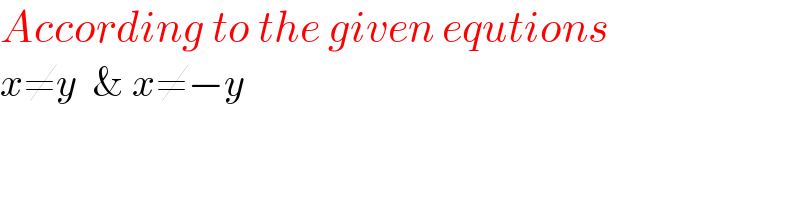
According to the given equtions x≠y & x≠−y

$${According}\:{to}\:{the}\:{given}\:{equtions}\: \\ $$$${x}\neq{y}\:\:\&\:{x}\neq−{y} \\ $$

Commented by Frix last updated on 20/Jul/23

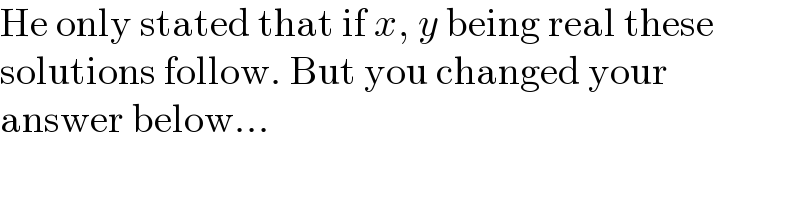
He only stated that if x, y being real these solutions follow. But you changed your answer below...

$$\mathrm{He}\:\mathrm{only}\:\mathrm{stated}\:\mathrm{that}\:\mathrm{if}\:{x},\:{y}\:\mathrm{being}\:\mathrm{real}\:\mathrm{these} \\ $$$$\mathrm{solutions}\:\mathrm{follow}.\:\mathrm{But}\:\mathrm{you}\:\mathrm{changed}\:\mathrm{your} \\ $$$$\mathrm{answer}\:\mathrm{below}... \\ $$

Answered by MM42 last updated on 20/Jul/23

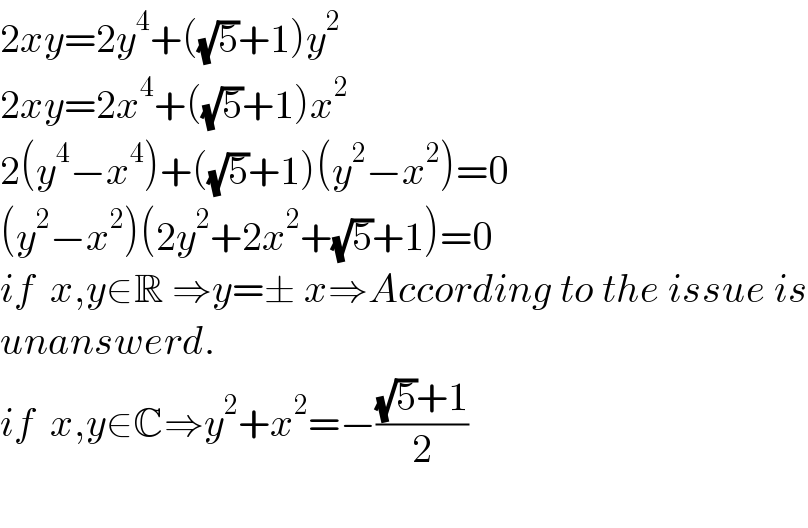
2xy=2y^4 +((√5)+1)y^2 2xy=2x^4 +((√5)+1)x^2 2(y^4 −x^4 )+((√5)+1)(y^2 −x^2 )=0 (y^2 −x^2 )(2y^2 +2x^2 +(√5)+1)=0 if x,y∈R ⇒y=± x⇒According to the issue is unanswerd. if x,y∈C⇒y^2 +x^2 =−(((√5)+1)/2)

$$\mathrm{2}{xy}=\mathrm{2}{y}^{\mathrm{4}} +\left(\sqrt{\mathrm{5}}+\mathrm{1}\right){y}^{\mathrm{2}} \\ $$$$\mathrm{2}{xy}=\mathrm{2}{x}^{\mathrm{4}} +\left(\sqrt{\mathrm{5}}+\mathrm{1}\right){x}^{\mathrm{2}} \\ $$$$\mathrm{2}\left({y}^{\mathrm{4}} −{x}^{\mathrm{4}} \right)+\left(\sqrt{\mathrm{5}}+\mathrm{1}\right)\left({y}^{\mathrm{2}} −{x}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\left({y}^{\mathrm{2}} −{x}^{\mathrm{2}} \right)\left(\mathrm{2}{y}^{\mathrm{2}} +\mathrm{2}{x}^{\mathrm{2}} +\sqrt{\mathrm{5}}+\mathrm{1}\right)=\mathrm{0} \\ $$$${if}\:\:{x},{y}\in\mathbb{R}\:\Rightarrow{y}=\pm\:{x}\Rightarrow{According}\:{to}\:{the}\:{issue}\:{is} \\ $$$${unanswerd}.\: \\ $$$${if}\:\:{x},{y}\in\mathbb{C}\Rightarrow{y}^{\mathrm{2}} +{x}^{\mathrm{2}} =−\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$

Commented by MJS_new last updated on 20/Jul/23

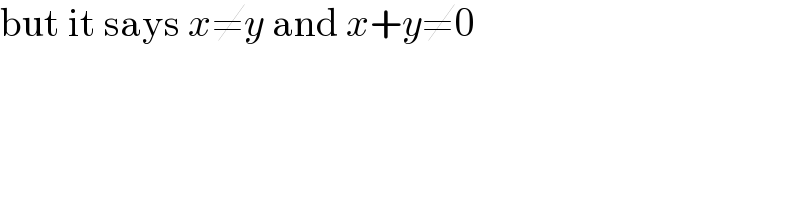
but it says x≠y and x+y≠0

$$\mathrm{but}\:\mathrm{it}\:\mathrm{says}\:{x}\neq{y}\:\mathrm{and}\:{x}+{y}\neq\mathrm{0} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com