Question and Answers Forum

All Questions      Topic List

Matrices and Determinants Questions

Previous in All Question      Next in All Question      

Previous in Matrices and Determinants      Next in Matrices and Determinants      

Question Number 194915 by York12 last updated on 19/Jul/23

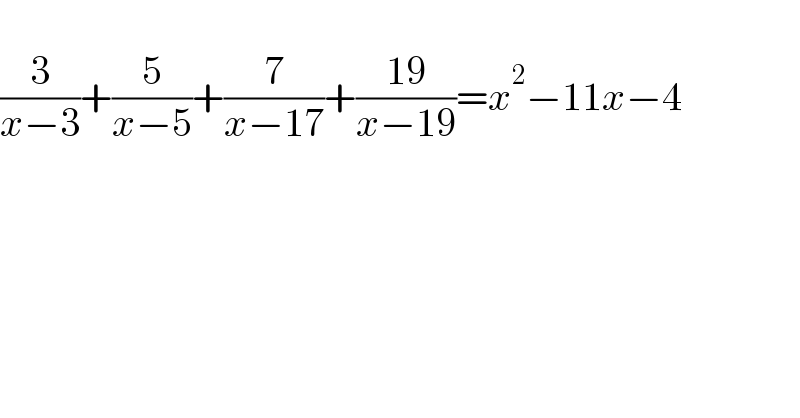
(3/(x−3))+(5/(x−5))+(7/(x−17))+((19)/(x−19))=x^2 −11x−4

$$ \\ $$$$\frac{\mathrm{3}}{{x}−\mathrm{3}}+\frac{\mathrm{5}}{{x}−\mathrm{5}}+\frac{\mathrm{7}}{{x}−\mathrm{17}}+\frac{\mathrm{19}}{{x}−\mathrm{19}}={x}^{\mathrm{2}} −\mathrm{11}{x}−\mathrm{4} \\ $$

Commented by BaliramKumar last updated on 19/Jul/23

typo 7→17

$$\mathrm{typo}\:\:\:\mathrm{7}\rightarrow\mathrm{17} \\ $$

Commented by York12 last updated on 19/Jul/23

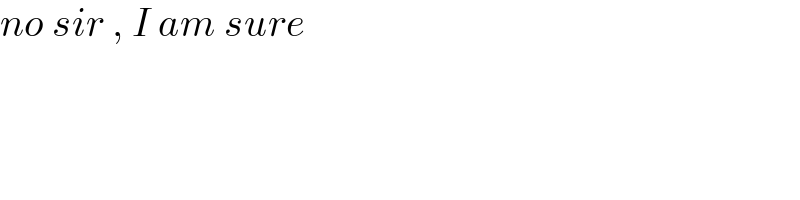
no sir , I am sure

$${no}\:{sir}\:,\:{I}\:{am}\:{sure} \\ $$

Commented by BaliramKumar last updated on 19/Jul/23

i guess just

$$\mathrm{i}\:\mathrm{guess}\:\mathrm{just} \\ $$

Commented by justenspi last updated on 19/Jul/23

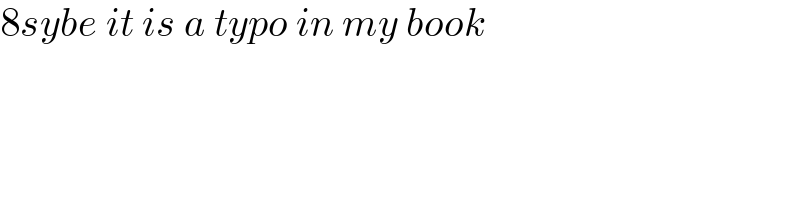
8sybe it is a typo in my book

$$\mathrm{8}{sybe}\:{it}\:{is}\:{a}\:{typo}\:{in}\:{my}\:{book} \\ $$

Answered by Rasheed.Sindhi last updated on 19/Jul/23

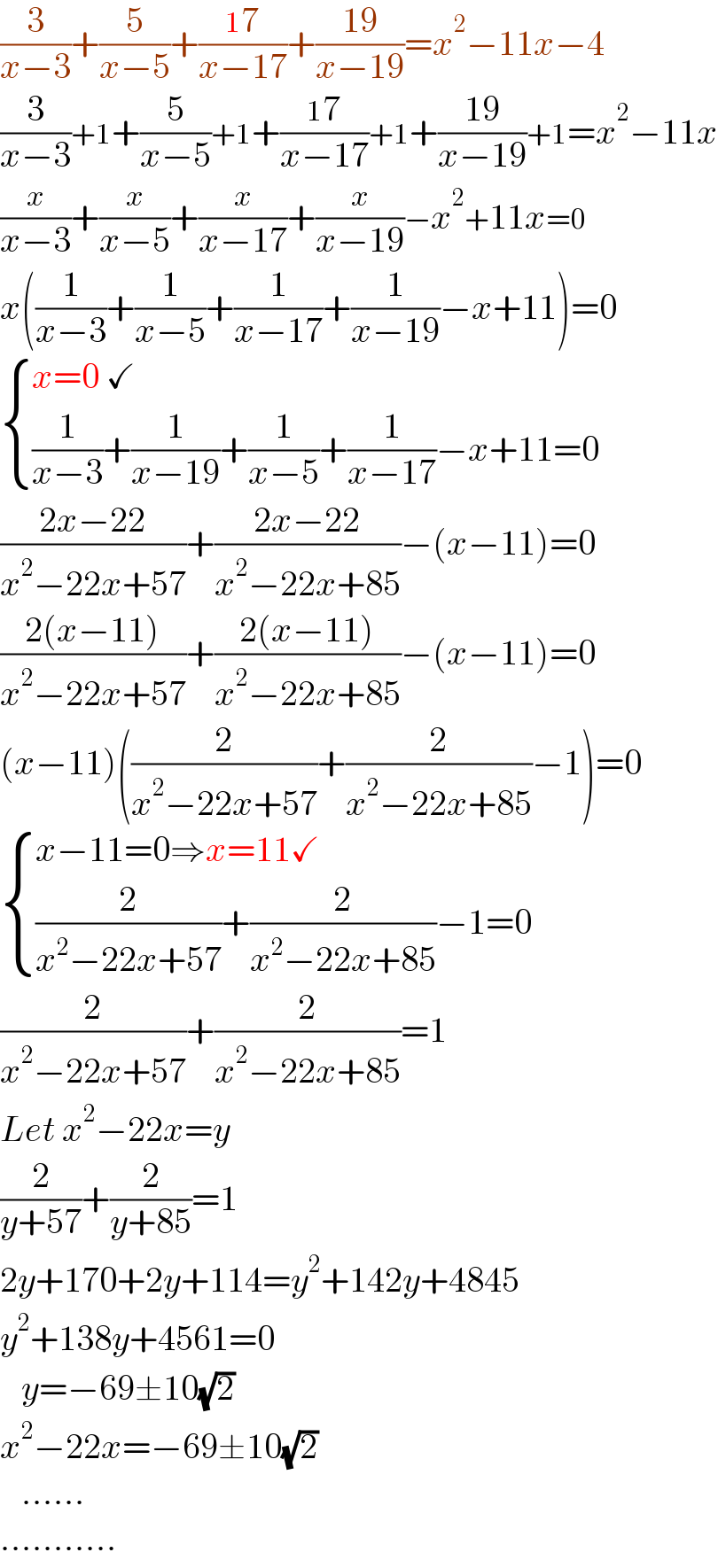
(3/(x−3))+(5/(x−5))+((17)/(x−17))+((19)/(x−19))=x^2 −11x−4 (3/(x−3))+1+(5/(x−5))+1+((17)/(x−17))+1+((19)/(x−19))+1=x^2 −11x (x/(x−3))+(x/(x−5))+(x/(x−17))+(x/(x−19))−x^2 +11x=0 x((1/(x−3))+(1/(x−5))+(1/(x−17))+(1/(x−19))−x+11)=0 { ((x=0 ✓)),(((1/(x−3))+(1/(x−19))+(1/(x−5))+(1/(x−17))−x+11=0)) :} ((2x−22)/(x^2 −22x+57))+((2x−22)/(x^2 −22x+85))−(x−11)=0 ((2(x−11))/(x^2 −22x+57))+((2(x−11))/(x^2 −22x+85))−(x−11)=0 (x−11)((2/(x^2 −22x+57))+(2/(x^2 −22x+85))−1)=0 { ((x−11=0⇒x=11✓)),(((2/(x^2 −22x+57))+(2/(x^2 −22x+85))−1=0)) :} (2/(x^2 −22x+57))+(2/(x^2 −22x+85))=1 Let x^2 −22x=y (2/(y+57))+(2/(y+85))=1 2y+170+2y+114=y^2 +142y+4845 y^2 +138y+4561=0 y=−69±10(√2) x^2 −22x=−69±10(√2) ...... ...........

$$\frac{\mathrm{3}}{{x}−\mathrm{3}}+\frac{\mathrm{5}}{{x}−\mathrm{5}}+\frac{\mathrm{17}}{{x}−\mathrm{17}}+\frac{\mathrm{19}}{{x}−\mathrm{19}}={x}^{\mathrm{2}} −\mathrm{11}{x}−\mathrm{4} \\ $$$$\frac{\mathrm{3}}{{x}−\mathrm{3}}+\mathrm{1}+\frac{\mathrm{5}}{{x}−\mathrm{5}}+\mathrm{1}+\frac{\mathrm{17}}{{x}−\mathrm{17}}+\mathrm{1}+\frac{\mathrm{19}}{{x}−\mathrm{19}}+\mathrm{1}={x}^{\mathrm{2}} −\mathrm{11}{x} \\ $$$$\frac{{x}}{{x}−\mathrm{3}}+\frac{{x}}{{x}−\mathrm{5}}+\frac{{x}}{{x}−\mathrm{17}}+\frac{{x}}{{x}−\mathrm{19}}−{x}^{\mathrm{2}} +\mathrm{11}{x}=\mathrm{0} \\ $$$${x}\left(\frac{\mathrm{1}}{{x}−\mathrm{3}}+\frac{\mathrm{1}}{{x}−\mathrm{5}}+\frac{\mathrm{1}}{{x}−\mathrm{17}}+\frac{\mathrm{1}}{{x}−\mathrm{19}}−{x}+\mathrm{11}\right)=\mathrm{0} \\ $$$$\begin{cases}{{x}=\mathrm{0}\:\checkmark}\\{\frac{\mathrm{1}}{{x}−\mathrm{3}}+\frac{\mathrm{1}}{{x}−\mathrm{19}}+\frac{\mathrm{1}}{{x}−\mathrm{5}}+\frac{\mathrm{1}}{{x}−\mathrm{17}}−{x}+\mathrm{11}=\mathrm{0}}\end{cases} \\ $$$$\frac{\mathrm{2}{x}−\mathrm{22}}{{x}^{\mathrm{2}} −\mathrm{22}{x}+\mathrm{57}}+\frac{\mathrm{2}{x}−\mathrm{22}}{{x}^{\mathrm{2}} −\mathrm{22}{x}+\mathrm{85}}−\left({x}−\mathrm{11}\right)=\mathrm{0} \\ $$$$\frac{\mathrm{2}\left({x}−\mathrm{11}\right)}{{x}^{\mathrm{2}} −\mathrm{22}{x}+\mathrm{57}}+\frac{\mathrm{2}\left({x}−\mathrm{11}\right)}{{x}^{\mathrm{2}} −\mathrm{22}{x}+\mathrm{85}}−\left({x}−\mathrm{11}\right)=\mathrm{0} \\ $$$$\left({x}−\mathrm{11}\right)\left(\frac{\mathrm{2}}{{x}^{\mathrm{2}} −\mathrm{22}{x}+\mathrm{57}}+\frac{\mathrm{2}}{{x}^{\mathrm{2}} −\mathrm{22}{x}+\mathrm{85}}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\begin{cases}{{x}−\mathrm{11}=\mathrm{0}\Rightarrow{x}=\mathrm{11}\checkmark}\\{\frac{\mathrm{2}}{{x}^{\mathrm{2}} −\mathrm{22}{x}+\mathrm{57}}+\frac{\mathrm{2}}{{x}^{\mathrm{2}} −\mathrm{22}{x}+\mathrm{85}}−\mathrm{1}=\mathrm{0}}\end{cases} \\ $$$$\frac{\mathrm{2}}{{x}^{\mathrm{2}} −\mathrm{22}{x}+\mathrm{57}}+\frac{\mathrm{2}}{{x}^{\mathrm{2}} −\mathrm{22}{x}+\mathrm{85}}=\mathrm{1} \\ $$$${Let}\:{x}^{\mathrm{2}} −\mathrm{22}{x}={y} \\ $$$$\frac{\mathrm{2}}{{y}+\mathrm{57}}+\frac{\mathrm{2}}{{y}+\mathrm{85}}=\mathrm{1} \\ $$$$\mathrm{2}{y}+\mathrm{170}+\mathrm{2}{y}+\mathrm{114}={y}^{\mathrm{2}} +\mathrm{142}{y}+\mathrm{4845} \\ $$$${y}^{\mathrm{2}} +\mathrm{138}{y}+\mathrm{4561}=\mathrm{0} \\ $$$$\:\:\:{y}=−\mathrm{69}\pm\mathrm{10}\sqrt{\mathrm{2}}\: \\ $$$${x}^{\mathrm{2}} −\mathrm{22}{x}=−\mathrm{69}\pm\mathrm{10}\sqrt{\mathrm{2}}\: \\ $$$$\:\:\:...... \\ $$$$........... \\ $$

Commented by York12 last updated on 19/Jul/23

tbanks

$${tbanks} \\ $$

Commented by BaliramKumar last updated on 19/Jul/23

Nice approach

$$\mathrm{Nice}\:\mathrm{approach} \\ $$

Commented by Rasheed.Sindhi last updated on 20/Jul/23

🙏

🙏

Answered by Rasheed.Sindhi last updated on 20/Jul/23

(3/(x−3))+((19)/(x−19))+(5/(x−5))+((17)/(x−17))=x^2 −11x−4 ((3x−57+19x−57)/(x^2 −22x+57))+((5x−85+17x−85)/(x^2 −22x+85))=x^2 −11x−4 ((22x−114)/(x^2 −22x+57))+2+((22x−170)/(x^2 −22x+85))+2=x^2 −11x ((2x^2 −22x)/(x^2 −22x+57))+((2x^2 −22x)/(x^2 −22x+85))−(x−11)x=0 x(x−11)((2/(x^2 −22x+57))+(2/(x^2 −22x+85))−1)=0 x=0,x=11, (2/(x^2 −22x+57))+(2/(x^2 −22x+85))−1=0 Let x^2 −22x=y (2/(y+57))+(2/(y+85))=1 2y+170+2y+114=y^2 +142y+4845 y^2 +138y+4561=0 y=−69±10(√2) x^2 −22x=−69±10(√2)

$$\frac{\mathrm{3}}{{x}−\mathrm{3}}+\frac{\mathrm{19}}{{x}−\mathrm{19}}+\frac{\mathrm{5}}{{x}−\mathrm{5}}+\frac{\mathrm{17}}{{x}−\mathrm{17}}={x}^{\mathrm{2}} −\mathrm{11}{x}−\mathrm{4} \\ $$$$\frac{\mathrm{3}{x}−\mathrm{57}+\mathrm{19}{x}−\mathrm{57}}{{x}^{\mathrm{2}} −\mathrm{22}{x}+\mathrm{57}}+\frac{\mathrm{5}{x}−\mathrm{85}+\mathrm{17}{x}−\mathrm{85}}{{x}^{\mathrm{2}} −\mathrm{22}{x}+\mathrm{85}}={x}^{\mathrm{2}} −\mathrm{11}{x}−\mathrm{4} \\ $$$$\frac{\mathrm{22}{x}−\mathrm{114}}{{x}^{\mathrm{2}} −\mathrm{22}{x}+\mathrm{57}}+\mathrm{2}+\frac{\mathrm{22}{x}−\mathrm{170}}{{x}^{\mathrm{2}} −\mathrm{22}{x}+\mathrm{85}}+\mathrm{2}={x}^{\mathrm{2}} −\mathrm{11}{x} \\ $$$$\frac{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{22}{x}}{{x}^{\mathrm{2}} −\mathrm{22}{x}+\mathrm{57}}+\frac{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{22}{x}}{{x}^{\mathrm{2}} −\mathrm{22}{x}+\mathrm{85}}−\left({x}−\mathrm{11}\right){x}=\mathrm{0} \\ $$$${x}\left({x}−\mathrm{11}\right)\left(\frac{\mathrm{2}}{{x}^{\mathrm{2}} −\mathrm{22}{x}+\mathrm{57}}+\frac{\mathrm{2}}{{x}^{\mathrm{2}} −\mathrm{22}{x}+\mathrm{85}}−\mathrm{1}\right)=\mathrm{0} \\ $$$${x}=\mathrm{0},{x}=\mathrm{11},\:\frac{\mathrm{2}}{{x}^{\mathrm{2}} −\mathrm{22}{x}+\mathrm{57}}+\frac{\mathrm{2}}{{x}^{\mathrm{2}} −\mathrm{22}{x}+\mathrm{85}}−\mathrm{1}=\mathrm{0} \\ $$$${Let}\:{x}^{\mathrm{2}} −\mathrm{22}{x}={y} \\ $$$$\frac{\mathrm{2}}{{y}+\mathrm{57}}+\frac{\mathrm{2}}{{y}+\mathrm{85}}=\mathrm{1} \\ $$$$\mathrm{2}{y}+\mathrm{170}+\mathrm{2}{y}+\mathrm{114}={y}^{\mathrm{2}} +\mathrm{142}{y}+\mathrm{4845} \\ $$$${y}^{\mathrm{2}} +\mathrm{138}{y}+\mathrm{4561}=\mathrm{0} \\ $$$${y}=−\mathrm{69}\pm\mathrm{10}\sqrt{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} −\mathrm{22}{x}=−\mathrm{69}\pm\mathrm{10}\sqrt{\mathrm{2}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com