
Question Number 194899 by kapoorshah last updated on 19/Jul/23
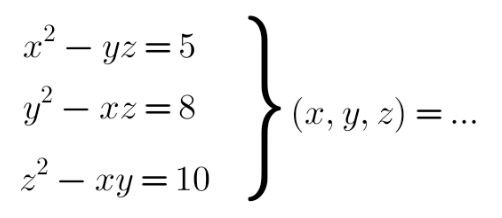
Answered by Frix last updated on 19/Jul/23
![y=px∧z=qx ⇒ x^2 =(5/(1−pq))=(8/(p^2 −q))=((10)/(q^2 −p)) (5/(1−pq))=(8/(p^2 −q)) ⇒ q=((8−5p^2 )/(8p−5)) Inserting in (5/(1−pq))=((10)/(q^2 −p)) and transforming p^4 +((14p^3 )/(55))=p+((14)/(55)) ⇒ p=−((14)/(55)) [∨p=1∨p=−(1/2)±((√3)/2)i _(the given eqs)^(don′t satisfy) ] Testing all solutions we get q=−((12)/(11)) x=±((55)/( (√(437))))∧y=∓((14)/( (√(437))))∧z=∓((60)/( (√(437))))](Q194905.png)
$${y}={px}\wedge{z}={qx} \\ $$$$\Rightarrow \\ $$$${x}^{\mathrm{2}} =\frac{\mathrm{5}}{\mathrm{1}−{pq}}=\frac{\mathrm{8}}{{p}^{\mathrm{2}} −{q}}=\frac{\mathrm{10}}{{q}^{\mathrm{2}} −{p}} \\ $$$$\frac{\mathrm{5}}{\mathrm{1}−{pq}}=\frac{\mathrm{8}}{{p}^{\mathrm{2}} −{q}}\:\Rightarrow\:{q}=\frac{\mathrm{8}−\mathrm{5}{p}^{\mathrm{2}} }{\mathrm{8}{p}−\mathrm{5}} \\ $$$$\mathrm{Inserting}\:\mathrm{in}\:\frac{\mathrm{5}}{\mathrm{1}−{pq}}=\frac{\mathrm{10}}{{q}^{\mathrm{2}} −{p}}\:\mathrm{and}\:\mathrm{transforming} \\ $$$${p}^{\mathrm{4}} +\frac{\mathrm{14}{p}^{\mathrm{3}} }{\mathrm{55}}={p}+\frac{\mathrm{14}}{\mathrm{55}} \\ $$$$\Rightarrow\:{p}=−\frac{\mathrm{14}}{\mathrm{55}}\:\left[\vee{p}=\mathrm{1}\vee{p}=−\frac{\mathrm{1}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\:_{\mathrm{the}\:\mathrm{given}\:\mathrm{eqs}} ^{\mathrm{don}'\mathrm{t}\:\mathrm{satisfy}} \right] \\ $$$$\mathrm{Testing}\:\mathrm{all}\:\mathrm{solutions}\:\mathrm{we}\:\mathrm{get} \\ $$$${q}=−\frac{\mathrm{12}}{\mathrm{11}} \\ $$$${x}=\pm\frac{\mathrm{55}}{\:\sqrt{\mathrm{437}}}\wedge{y}=\mp\frac{\mathrm{14}}{\:\sqrt{\mathrm{437}}}\wedge{z}=\mp\frac{\mathrm{60}}{\:\sqrt{\mathrm{437}}} \\ $$
Commented by kapoorshah last updated on 19/Jul/23

$${nice} \\ $$$${thank}\:{you} \\ $$
