
Question Number 194812 by sonukgindia last updated on 16/Jul/23
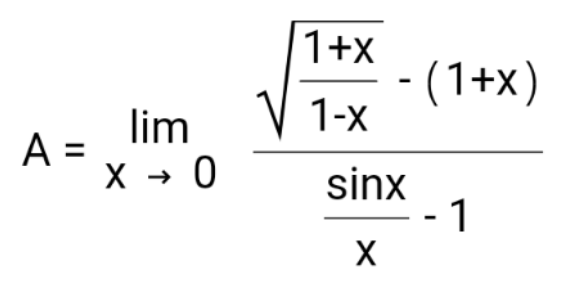
Answered by MM42 last updated on 16/Jul/23
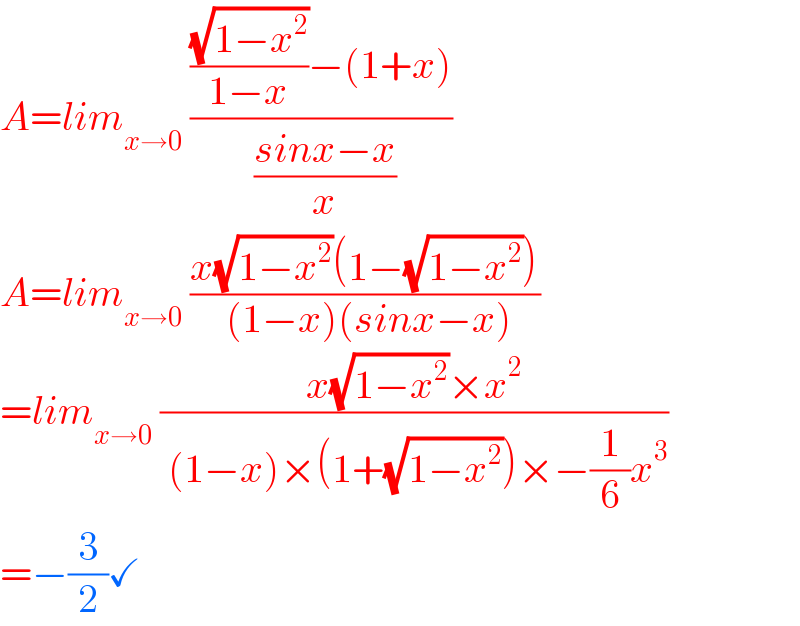
$${A}={lim}_{{x}\rightarrow\mathrm{0}} \:\frac{\frac{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{\mathrm{1}−{x}}−\left(\mathrm{1}+{x}\right)}{\:\frac{{sinx}−{x}}{{x}}} \\ $$$${A}={lim}_{{x}\rightarrow\mathrm{0}} \:\frac{{x}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\left(\mathrm{1}−\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\right)}{\:\left(\mathrm{1}−{x}\right)\left({sinx}−{x}\right)} \\ $$$$={lim}_{{x}\rightarrow\mathrm{0}} \:\frac{{x}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }×{x}^{\mathrm{2}} }{\:\left(\mathrm{1}−{x}\right)×\left(\mathrm{1}+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\right)×−\frac{\mathrm{1}}{\mathrm{6}}{x}^{\mathrm{3}} }\: \\ $$$$=−\frac{\mathrm{3}}{\mathrm{2}}\checkmark \\ $$
Answered by cortano12 last updated on 18/Jul/23
$$\:\: \underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}}−\left(\mathrm{1}+{x}\right)}{\frac{\mathrm{sin}\:{x}}{{x}}−\mathrm{1}} \\ $$$$\:\:\:\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{1}+{x}}−\left(\mathrm{1}+{x}\right)\sqrt{\mathrm{1}−{x}}}{\:\sqrt{\mathrm{1}−{x}}\:\left(\frac{\mathrm{sin}\:{x}−{x}}{{x}}\right)} \\ $$$$\:\:\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{1}+{x}}\:\left(\mathrm{1}−\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:\right)}{\:\sqrt{\mathrm{1}−{x}}\:\left(\frac{\mathrm{sin}\:{x}−{x}}{{x}}\right)} \\ $$$$\:\:\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{1}−{x}}}{\:\sqrt{\mathrm{1}−{x}}}\:.\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}^{\mathrm{3}} }{\left(\mathrm{1}+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\right)\left(\mathrm{sin}\:{x}−{x}\right)} \\ $$$$\:\:\:=\:\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{1}}{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{sin}\:{x}−{x}}{{x}^{\mathrm{3}} }\right)} \\ $$$$\:\:=\:\begin{array}{|c|}{\frac{\mathrm{1}}{\mathrm{2}}.\left(\frac{\mathrm{1}}{−\mathrm{1}/\mathrm{6}}\right)=\:−\mathrm{3}}\\\hline\end{array} \\ $$$$\:\: \\ $$$$ \\ $$
