Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 194113 by Rupesh123 last updated on 28/Jun/23

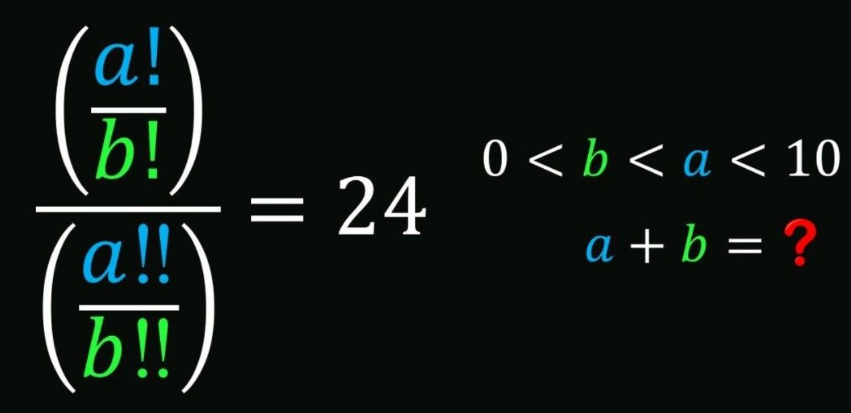
Answered by Subhi last updated on 28/Jun/23

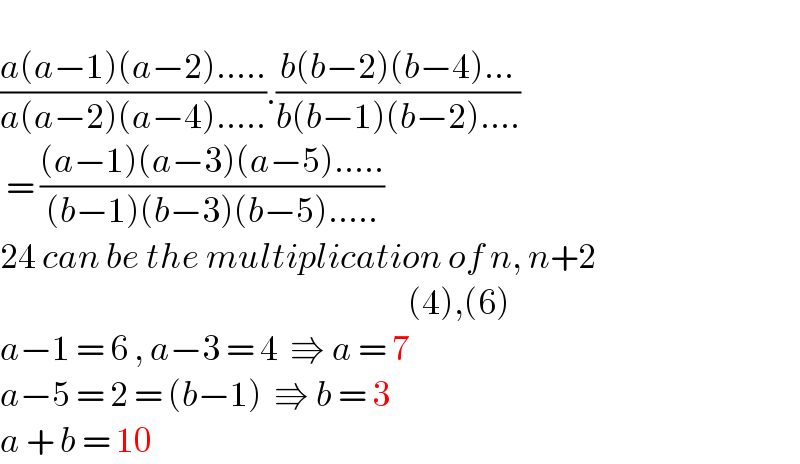
((a(a−1)(a−2).....)/(a(a−2)(a−4).....)).((b(b−2)(b−4)...)/(b(b−1)(b−2)....)) = (((a−1)(a−3)(a−5).....)/((b−1)(b−3)(b−5).....)) 24 can be the multiplication of n, n+2 (4),(6) a−1 = 6 , a−3 = 4 ⇛ a = 7 a−5 = 2 = (b−1) ⇛ b = 3 a + b = 10

$$ \\ $$$$\frac{{a}\left({a}−\mathrm{1}\right)\left({a}−\mathrm{2}\right).....}{{a}\left({a}−\mathrm{2}\right)\left({a}−\mathrm{4}\right).....}.\frac{{b}\left({b}−\mathrm{2}\right)\left({b}−\mathrm{4}\right)...}{{b}\left({b}−\mathrm{1}\right)\left({b}−\mathrm{2}\right)....} \\ $$$$\:=\:\frac{\left({a}−\mathrm{1}\right)\left({a}−\mathrm{3}\right)\left({a}−\mathrm{5}\right).....}{\left({b}−\mathrm{1}\right)\left({b}−\mathrm{3}\right)\left({b}−\mathrm{5}\right).....}\:\:\:\: \\ $$$$\mathrm{24}\:{can}\:{be}\:{the}\:{multiplication}\:{of}\:{n},\:{n}+\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{4}\right),\left(\mathrm{6}\right) \\ $$$${a}−\mathrm{1}\:=\:\mathrm{6}\:,\:{a}−\mathrm{3}\:=\:\mathrm{4}\:\:\Rrightarrow\:{a}\:=\:\mathrm{7} \\ $$$${a}−\mathrm{5}\:=\:\mathrm{2}\:=\:\left({b}−\mathrm{1}\right)\:\:\Rrightarrow\:{b}\:=\:\mathrm{3} \\ $$$${a}\:+\:{b}\:=\:\mathrm{10} \\ $$

Commented by Rupesh123 last updated on 28/Jun/23

Perfect ��

Terms of Service

Privacy Policy

Contact: info@tinkutara.com