
Question Number 194086 by mathlove last updated on 27/Jun/23
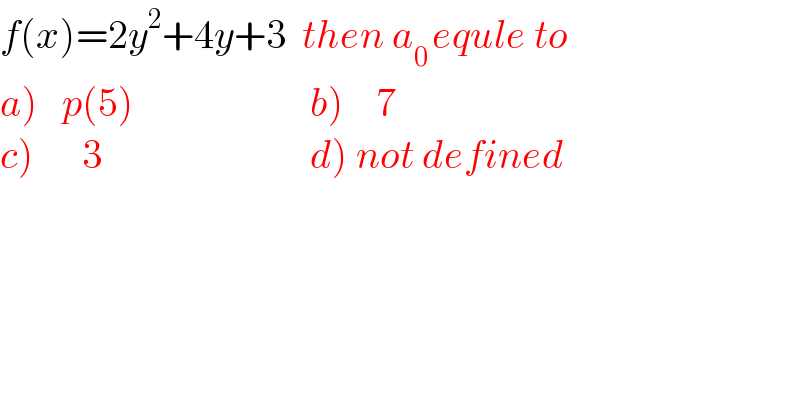
$${f}\left({x}\right)=\mathrm{2}{y}^{\mathrm{2}} +\mathrm{4}{y}+\mathrm{3}\:\:{then}\:{a}_{\mathrm{0}\:} {equle}\:{to} \\ $$$$\left.{a}\left.\right)\:\:\:{p}\left(\mathrm{5}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{b}\right)\:\:\:\:\mathrm{7} \\ $$$$\left.{c}\left.\right)\:\:\:\:\:\:\mathrm{3}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{d}\right)\:{not}\:{defined} \\ $$
Commented by Frix last updated on 27/Jun/23
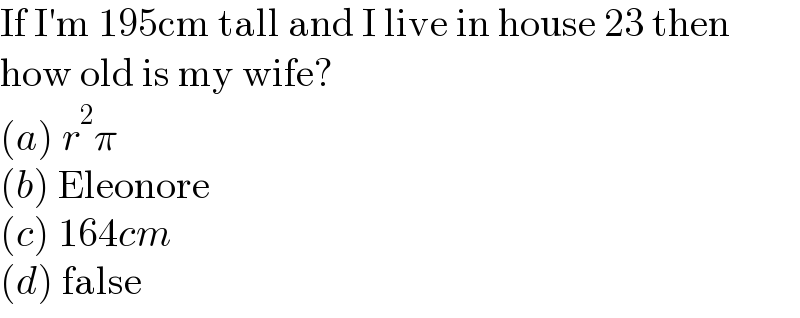
$$\mathrm{If}\:\mathrm{I}'\mathrm{m}\:\mathrm{195cm}\:\mathrm{tall}\:\mathrm{and}\:\mathrm{I}\:\mathrm{live}\:\mathrm{in}\:\mathrm{house}\:\mathrm{23}\:\mathrm{then} \\ $$$$\mathrm{how}\:\mathrm{old}\:\mathrm{is}\:\mathrm{my}\:\mathrm{wife}? \\ $$$$\left({a}\right)\:{r}^{\mathrm{2}} \pi \\ $$$$\left({b}\right)\:\mathrm{Eleonore} \\ $$$$\left({c}\right)\:\mathrm{164}{cm} \\ $$$$\left({d}\right)\:\mathrm{false} \\ $$
Answered by MikeH last updated on 30/Jun/23

$$\mathrm{This}\:\mathrm{is}\:\mathrm{the}\:\mathrm{most}\:\mathrm{hilarious}\:\mathrm{question} \\ $$$$\mathrm{I}'\mathrm{ve}\:\mathrm{ever}\:\mathrm{seen}\:\mathrm{LOL}. \\ $$$$\mathrm{I}\:\mathrm{simply}\:\mathrm{believe}\:\mathrm{you}'\mathrm{re}\:\mathrm{tryna}\:\mathrm{have}\:\mathrm{the}\:\mathrm{standard} \\ $$$$\mathrm{form}\:\mathrm{of}\:\mathrm{quadratic}\:\mathrm{function}\:\left({f}\left({x}\right)\:=\:{a}_{\mathrm{2}} {x}^{\mathrm{2}} +{a}_{\mathrm{1}} {x}\:+\:{a}_{\mathrm{0}} \right) \\ $$$$\mathrm{but}\:\mathrm{dude}!!\:\mathrm{Define}\:\mathrm{things}\:\mathrm{properly} \\ $$$$ \\ $$
Commented by mathlove last updated on 02/Jul/23

$${tnk} \\ $$
