Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 193962 by Abdullahrussell last updated on 24/Jun/23

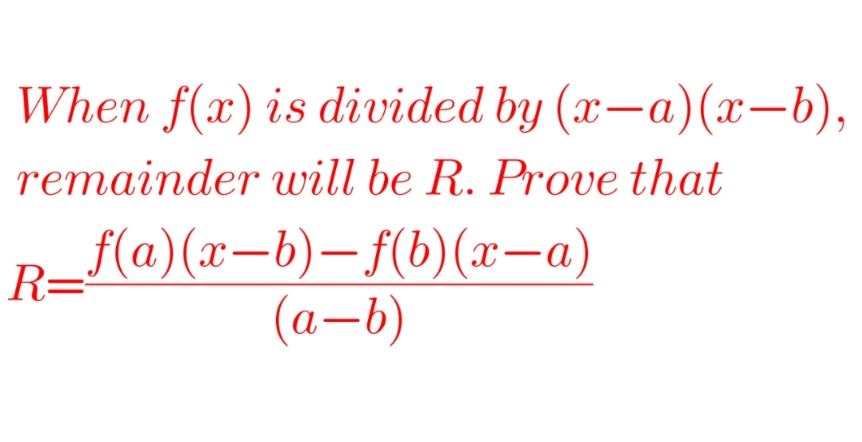
Answered by deleteduser1 last updated on 24/Jun/23

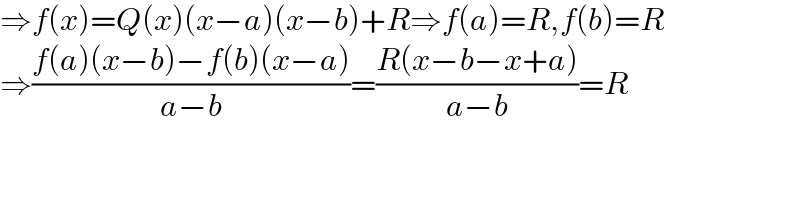
⇒f(x)=Q(x)(x−a)(x−b)+R⇒f(a)=R,f(b)=R ⇒((f(a)(x−b)−f(b)(x−a))/(a−b))=((R(x−b−x+a))/(a−b))=R

$$\Rightarrow{f}\left({x}\right)={Q}\left({x}\right)\left({x}−{a}\right)\left({x}−{b}\right)+{R}\Rightarrow{f}\left({a}\right)={R},{f}\left({b}\right)={R} \\ $$$$\Rightarrow\frac{{f}\left({a}\right)\left({x}−{b}\right)−{f}\left({b}\right)\left({x}−{a}\right)}{{a}−{b}}=\frac{{R}\left({x}−{b}−{x}+{a}\right)}{{a}−{b}}={R} \\ $$

Answered by cortano12 last updated on 24/Jun/23

x=a⇒f(a)= ma+n x=b⇒f(b)=mb+n ⇒ { ((m=((f(a)−f(b))/(a−b)))),((n=f(a)−a(((f(a)−f(b))/(a−b))))) :} ⇒n=((af(a)−bf(a)−af(a)+af(b))/(a−b)) ⇒n= ((af(b)−bf(a))/(a−b)) (((f(a)−f(b))/(a−b)))x+((af(b)−bf(a))/(a−b)) determinant (((R=((f(a)(x−b)−f(b)(x−a))/(a−b)))))

$$\:\:\: \\ $$$$ {x}={a}\Rightarrow\mathrm{f}\left({a}\right)=\:{ma}+{n} \\ $$$$\:{x}={b}\Rightarrow\mathrm{f}\left({b}\right)={mb}+{n}\: \\ $$$$\:\:\Rightarrow\begin{cases}{{m}=\frac{{f}\left({a}\right)−{f}\left({b}\right)}{{a}−{b}}}\\{{n}={f}\left({a}\right)−{a}\left(\frac{{f}\left({a}\right)−{f}\left({b}\right)}{{a}−{b}}\right)}\end{cases} \\ $$$$\:\:\Rightarrow{n}=\frac{{af}\left({a}\right)−{bf}\left({a}\right)−{af}\left({a}\right)+{af}\left({b}\right)}{{a}−{b}} \\ $$$$\:\:\Rightarrow{n}=\:\frac{{af}\left({b}\right)−{bf}\left({a}\right)}{{a}−{b}} \\ $$$$\: \\ $$$$ \left(\frac{{f}\left({a}\right)−{f}\left({b}\right)}{{a}−{b}}\right){x}+\frac{{af}\left({b}\right)−{bf}\left({a}\right)}{{a}−{b}} \\ $$$$\:\:\begin{array}{|c|}{\mathrm{R}=\frac{{f}\left({a}\right)\left({x}−{b}\right)−{f}\left({b}\right)\left({x}−{a}\right)}{{a}−{b}}}\\\hline\end{array} \\ $$$$ \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com