Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 193949 by sonukgindia last updated on 23/Jun/23

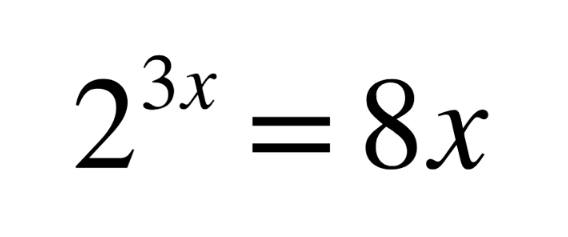
Answered by aleks041103 last updated on 23/Jun/23

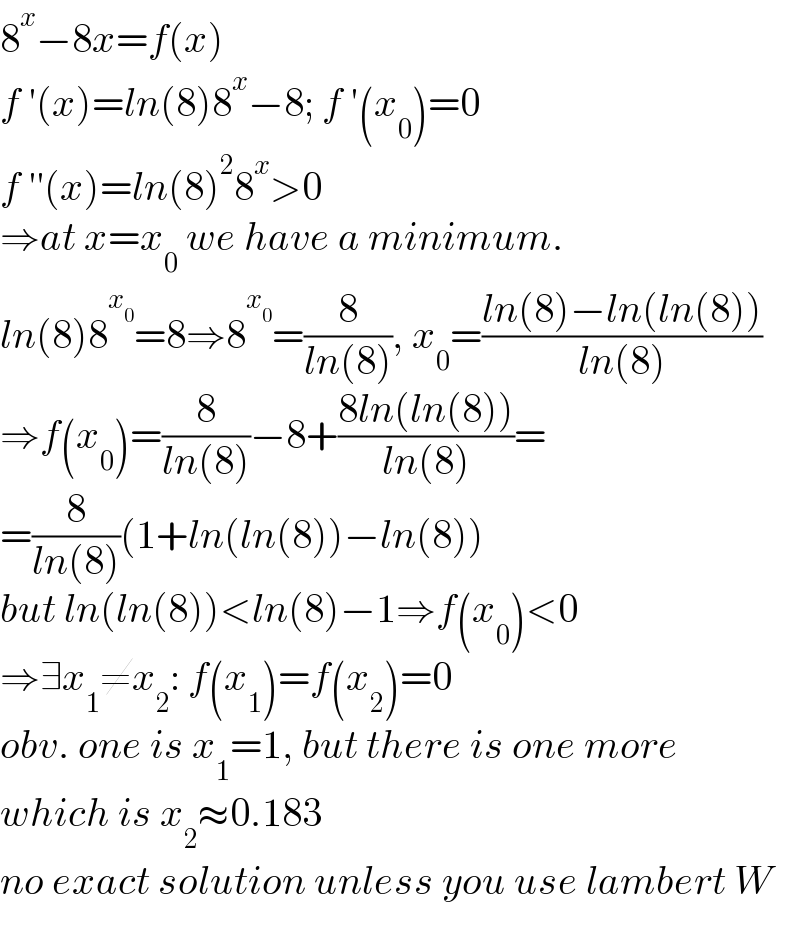
8^x −8x=f(x) f ′(x)=ln(8)8^x −8; f ′(x_0 )=0 f ′′(x)=ln(8)^2 8^x >0 ⇒at x=x_0 we have a minimum. ln(8)8^x_0 =8⇒8^x_0 =(8/(ln(8))), x_0 =((ln(8)−ln(ln(8)))/(ln(8))) ⇒f(x_0 )=(8/(ln(8)))−8+((8ln(ln(8)))/(ln(8)))= =(8/(ln(8)))(1+ln(ln(8))−ln(8)) but ln(ln(8))<ln(8)−1⇒f(x_0 )<0 ⇒∃x_1 ≠x_2 : f(x_1 )=f(x_2 )=0 obv. one is x_1 =1, but there is one more which is x_2 ≈0.183 no exact solution unless you use lambert W

$$\mathrm{8}^{{x}} −\mathrm{8}{x}={f}\left({x}\right) \\ $$$${f}\:'\left({x}\right)={ln}\left(\mathrm{8}\right)\mathrm{8}^{{x}} −\mathrm{8};\:{f}\:'\left({x}_{\mathrm{0}} \right)=\mathrm{0} \\ $$$${f}\:''\left({x}\right)={ln}\left(\mathrm{8}\right)^{\mathrm{2}} \mathrm{8}^{{x}} >\mathrm{0} \\ $$$$\Rightarrow{at}\:{x}={x}_{\mathrm{0}} \:{we}\:{have}\:{a}\:{minimum}. \\ $$$${ln}\left(\mathrm{8}\right)\mathrm{8}^{{x}_{\mathrm{0}} } =\mathrm{8}\Rightarrow\mathrm{8}^{{x}_{\mathrm{0}} } =\frac{\mathrm{8}}{{ln}\left(\mathrm{8}\right)},\:{x}_{\mathrm{0}} =\frac{{ln}\left(\mathrm{8}\right)−{ln}\left({ln}\left(\mathrm{8}\right)\right)}{{ln}\left(\mathrm{8}\right)} \\ $$$$\Rightarrow{f}\left({x}_{\mathrm{0}} \right)=\frac{\mathrm{8}}{{ln}\left(\mathrm{8}\right)}−\mathrm{8}+\frac{\mathrm{8}{ln}\left({ln}\left(\mathrm{8}\right)\right)}{{ln}\left(\mathrm{8}\right)}= \\ $$$$=\frac{\mathrm{8}}{{ln}\left(\mathrm{8}\right)}\left(\mathrm{1}+{ln}\left({ln}\left(\mathrm{8}\right)\right)−{ln}\left(\mathrm{8}\right)\right) \\ $$$${but}\:{ln}\left({ln}\left(\mathrm{8}\right)\right)<{ln}\left(\mathrm{8}\right)−\mathrm{1}\Rightarrow{f}\left({x}_{\mathrm{0}} \right)<\mathrm{0} \\ $$$$\Rightarrow\exists{x}_{\mathrm{1}} \neq{x}_{\mathrm{2}} :\:{f}\left({x}_{\mathrm{1}} \right)={f}\left({x}_{\mathrm{2}} \right)=\mathrm{0} \\ $$$${obv}.\:{one}\:{is}\:{x}_{\mathrm{1}} =\mathrm{1},\:{but}\:{there}\:{is}\:{one}\:{more} \\ $$$${which}\:{is}\:{x}_{\mathrm{2}} \approx\mathrm{0}.\mathrm{183} \\ $$$${no}\:{exact}\:{solution}\:{unless}\:{you}\:{use}\:{lambert}\:{W} \\ $$

Answered by Subhi last updated on 24/Jun/23

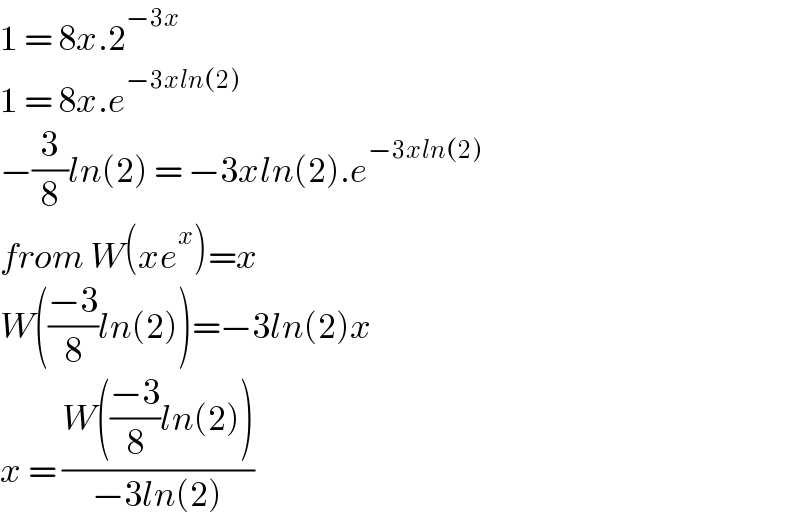
1 = 8x.2^(−3x) 1 = 8x.e^(−3xln(2)) −(3/8)ln(2) = −3xln(2).e^(−3xln(2)) from W(xe^x )=x W(((−3)/8)ln(2))=−3ln(2)x x = ((W(((−3)/8)ln(2)))/(−3ln(2)))

$$\mathrm{1}\:=\:\mathrm{8}{x}.\mathrm{2}^{−\mathrm{3}{x}} \:\: \\ $$$$\mathrm{1}\:=\:\mathrm{8}{x}.{e}^{−\mathrm{3}{xln}\left(\mathrm{2}\right)} \\ $$$$−\frac{\mathrm{3}}{\mathrm{8}}{ln}\left(\mathrm{2}\right)\:=\:−\mathrm{3}{xln}\left(\mathrm{2}\right).{e}^{−\mathrm{3}{xln}\left(\mathrm{2}\right)} \\ $$$${from}\:{W}\left({xe}^{{x}} \right)={x} \\ $$$${W}\left(\frac{−\mathrm{3}}{\mathrm{8}}{ln}\left(\mathrm{2}\right)\right)=−\mathrm{3}{ln}\left(\mathrm{2}\right){x} \\ $$$${x}\:=\:\frac{{W}\left(\frac{−\mathrm{3}}{\mathrm{8}}{ln}\left(\mathrm{2}\right)\right)}{−\mathrm{3}{ln}\left(\mathrm{2}\right)} \\ $$

Answered by Spillover last updated on 24/Jun/23

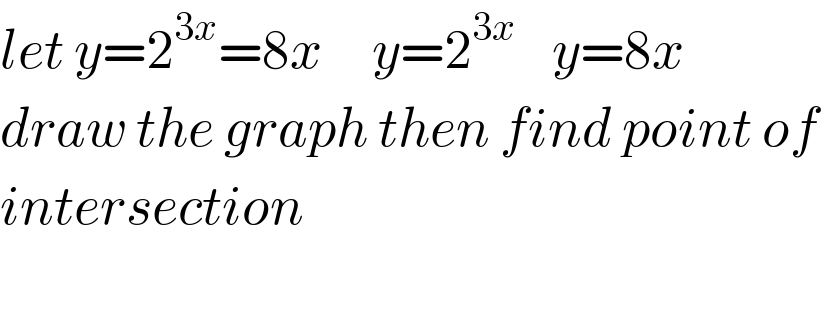
let y=2^(3x) =8x y=2^(3x ) y=8x draw the graph then find point of intersection

$${let}\:{y}=\mathrm{2}^{\mathrm{3}{x}} =\mathrm{8}{x}\:\:\:\:\:{y}=\mathrm{2}^{\mathrm{3}{x}\:\:} \:\:{y}=\mathrm{8}{x} \\ $$$${draw}\:{the}\:{graph}\:{then}\:{find}\:{point}\:{of}\: \\ $$$${intersection} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com