Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 193922 by sonukgindia last updated on 23/Jun/23

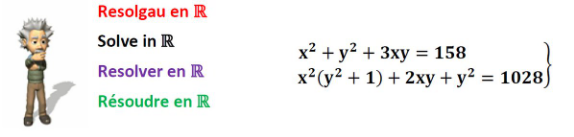
Answered by talminator2856792 last updated on 23/Jun/23

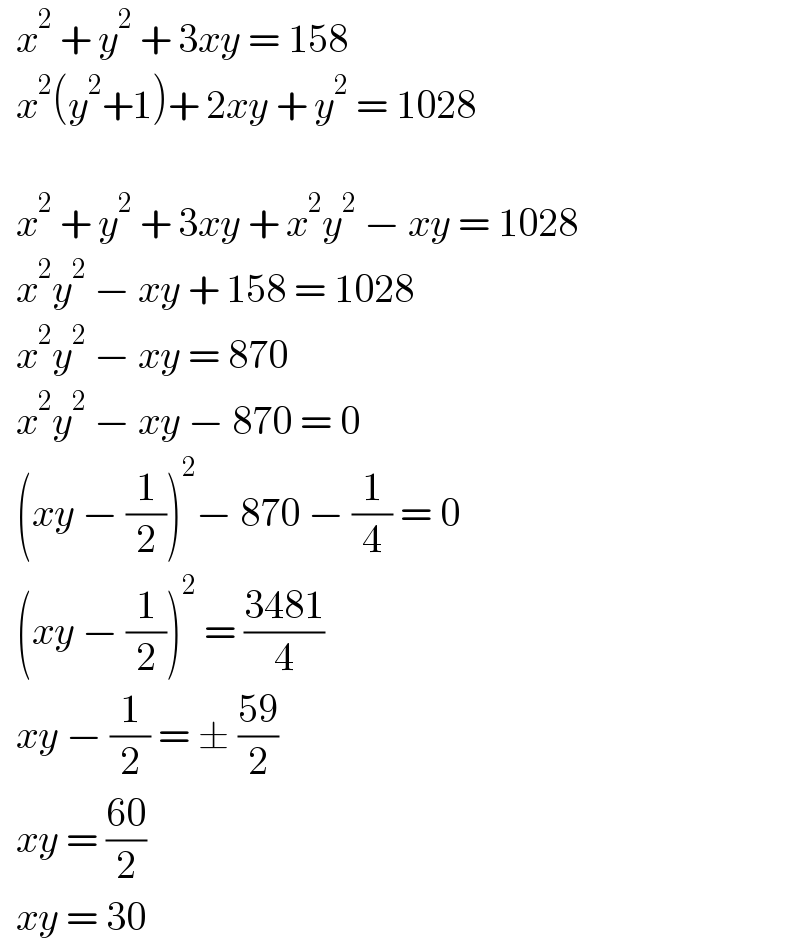
x^2 + y^2 + 3xy = 158 x^2 (y^2 +1)+ 2xy + y^2 = 1028 x^2 + y^2 + 3xy + x^2 y^2 − xy = 1028 x^2 y^2 − xy + 158 = 1028 x^2 y^2 − xy = 870 x^2 y^2 − xy − 870 = 0 (xy − (1/2))^2 − 870 − (1/4) = 0 (xy − (1/2))^2 = ((3481)/4) xy − (1/2) = ± ((59)/2) xy = ((60)/2) xy = 30

$$\:\:{x}^{\mathrm{2}} \:+\:{y}^{\mathrm{2}} \:+\:\mathrm{3}{xy}\:=\:\mathrm{158} \\ $$$$\:\:{x}^{\mathrm{2}} \left({y}^{\mathrm{2}} +\mathrm{1}\right)+\:\mathrm{2}{xy}\:+\:{y}^{\mathrm{2}} \:=\:\mathrm{1028} \\ $$$$\:\: \\ $$$$\:\:{x}^{\mathrm{2}} \:+\:{y}^{\mathrm{2}} \:+\:\mathrm{3}{xy}\:+\:{x}^{\mathrm{2}} {y}^{\mathrm{2}} \:−\:{xy}\:=\:\mathrm{1028}\:\:\:\: \\ $$$$\:\:{x}^{\mathrm{2}} {y}^{\mathrm{2}} \:−\:{xy}\:+\:\mathrm{158}\:=\:\mathrm{1028} \\ $$$$\:\:{x}^{\mathrm{2}} {y}^{\mathrm{2}} \:−\:{xy}\:=\:\mathrm{870} \\ $$$$\:\:{x}^{\mathrm{2}} {y}^{\mathrm{2}} \:−\:{xy}\:−\:\mathrm{870}\:=\:\mathrm{0} \\ $$$$\:\:\left({xy}\:−\:\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\:\mathrm{870}\:−\:\frac{\mathrm{1}}{\mathrm{4}}\:=\:\mathrm{0} \\ $$$$\:\:\left({xy}\:−\:\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:=\:\frac{\mathrm{3481}}{\mathrm{4}} \\ $$$$\:\:{xy}\:−\:\frac{\mathrm{1}}{\mathrm{2}}\:=\:\pm\:\frac{\mathrm{59}}{\mathrm{2}} \\ $$$$\:\:{xy}\:=\:\frac{\mathrm{60}}{\mathrm{2}} \\ $$$$\:\:{xy}\:=\:\mathrm{30} \\ $$

Answered by Rajpurohith last updated on 23/Jun/23

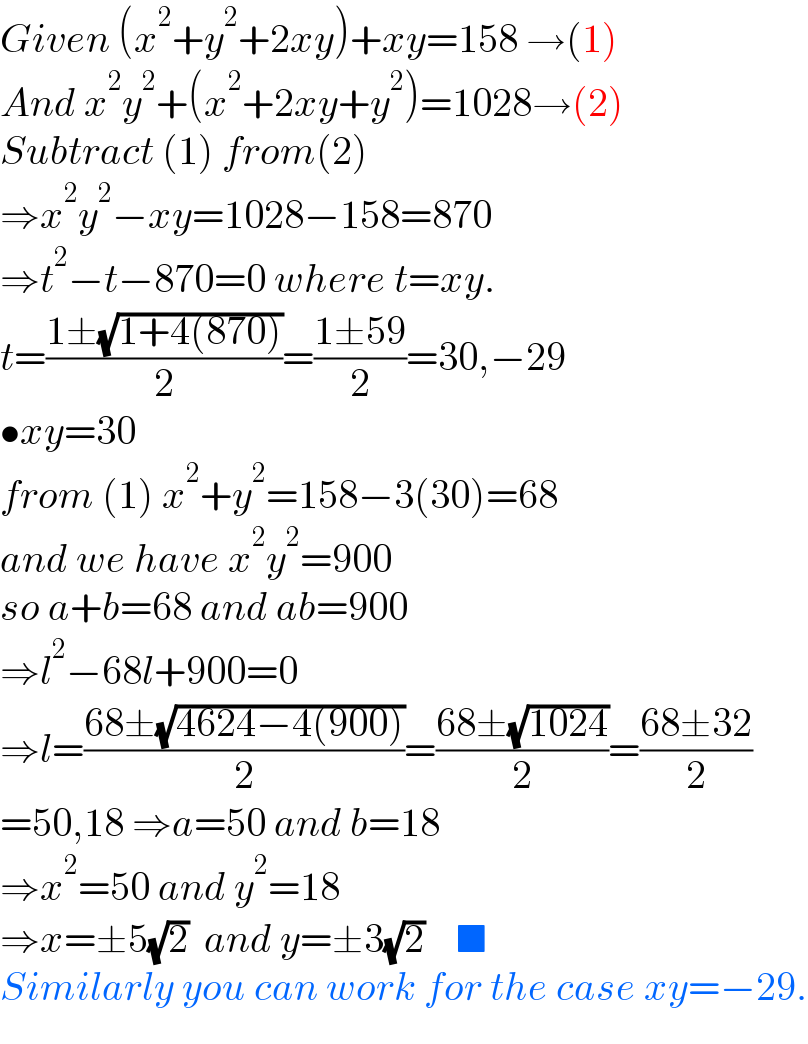
Given (x^2 +y^2 +2xy)+xy=158 →(1) And x^2 y^2 +(x^2 +2xy+y^2 )=1028→(2) Subtract (1) from(2) ⇒x^2 y^2 −xy=1028−158=870 ⇒t^2 −t−870=0 where t=xy. t=((1±(√(1+4(870))))/2)=((1±59)/2)=30,−29 •xy=30 from (1) x^2 +y^2 =158−3(30)=68 and we have x^2 y^2 =900 so a+b=68 and ab=900 ⇒l^2 −68l+900=0 ⇒l=((68±(√(4624−4(900))))/2)=((68±(√(1024)))/2)=((68±32)/2) =50,18 ⇒a=50 and b=18 ⇒x^2 =50 and y^2 =18 ⇒x=±5(√2) and y=±3(√2) ■ Similarly you can work for the case xy=−29.

$${Given}\:\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{2}{xy}\right)+{xy}=\mathrm{158}\:\rightarrow\left(\mathrm{1}\right) \\ $$$${And}\:{x}^{\mathrm{2}} {y}^{\mathrm{2}} +\left({x}^{\mathrm{2}} +\mathrm{2}{xy}+{y}^{\mathrm{2}} \right)=\mathrm{1028}\rightarrow\left(\mathrm{2}\right) \\ $$$${Subtract}\:\left(\mathrm{1}\right)\:{from}\left(\mathrm{2}\right) \\ $$$$\Rightarrow{x}^{\mathrm{2}} {y}^{\mathrm{2}} −{xy}=\mathrm{1028}−\mathrm{158}=\mathrm{870} \\ $$$$\Rightarrow{t}^{\mathrm{2}} −{t}−\mathrm{870}=\mathrm{0}\:{where}\:{t}={xy}. \\ $$$${t}=\frac{\mathrm{1}\pm\sqrt{\mathrm{1}+\mathrm{4}\left(\mathrm{870}\right)}}{\mathrm{2}}=\frac{\mathrm{1}\pm\mathrm{59}}{\mathrm{2}}=\mathrm{30},−\mathrm{29} \\ $$$$\bullet{xy}=\mathrm{30} \\ $$$${from}\:\left(\mathrm{1}\right)\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{158}−\mathrm{3}\left(\mathrm{30}\right)=\mathrm{68} \\ $$$${and}\:{we}\:{have}\:{x}^{\mathrm{2}} {y}^{\mathrm{2}} =\mathrm{900} \\ $$$${so}\:{a}+{b}=\mathrm{68}\:{and}\:{ab}=\mathrm{900} \\ $$$$\Rightarrow{l}^{\mathrm{2}} −\mathrm{68}{l}+\mathrm{900}=\mathrm{0} \\ $$$$\Rightarrow{l}=\frac{\mathrm{68}\pm\sqrt{\mathrm{4624}−\mathrm{4}\left(\mathrm{900}\right)}}{\mathrm{2}}=\frac{\mathrm{68}\pm\sqrt{\mathrm{1024}}}{\mathrm{2}}=\frac{\mathrm{68}\pm\mathrm{32}}{\mathrm{2}} \\ $$$$=\mathrm{50},\mathrm{18}\:\Rightarrow{a}=\mathrm{50}\:{and}\:{b}=\mathrm{18} \\ $$$$\Rightarrow{x}^{\mathrm{2}} =\mathrm{50}\:{and}\:{y}^{\mathrm{2}} =\mathrm{18} \\ $$$$\Rightarrow{x}=\pm\mathrm{5}\sqrt{\mathrm{2}}\:\:{and}\:{y}=\pm\mathrm{3}\sqrt{\mathrm{2}}\:\:\:\:\blacksquare \\ $$$${Similarly}\:{you}\:{can}\:{work}\:{for}\:{the}\:{case}\:{xy}=−\mathrm{29}. \\ $$

Answered by MM42 last updated on 23/Jun/23

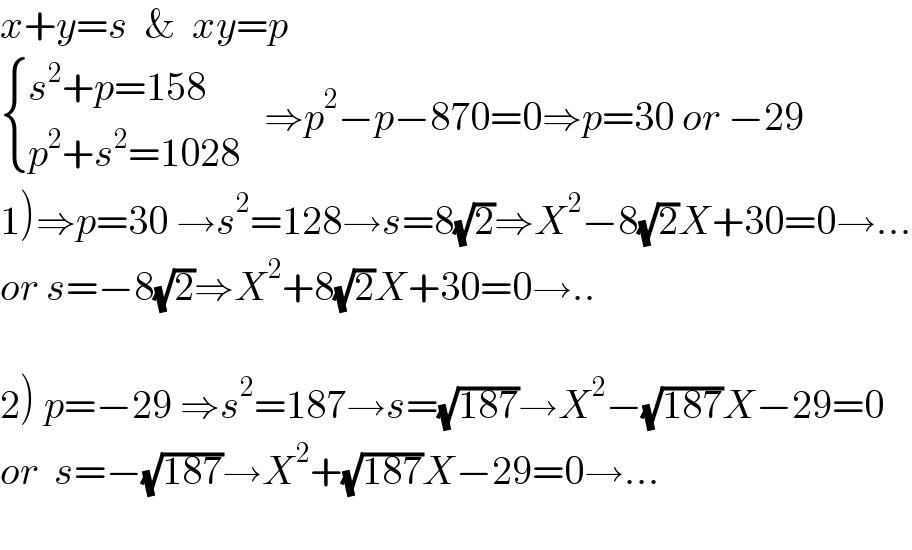
x+y=s & xy=p { ((s^2 +p=158)),((p^2 +s^2 =1028)) :} ⇒p^2 −p−870=0⇒p=30 or −29 1)⇒p=30 →s^2 =128→s=8(√2)⇒X^2 −8(√2)X+30=0→... or s=−8(√2)⇒X^2 +8(√2)X+30=0→.. 2) p=−29 ⇒s^2 =187→s=(√(187))→X^2 −(√(187))X−29=0 or s=−(√(187))→X^2 +(√(187))X−29=0→...

$${x}+{y}={s}\:\:\&\:\:{xy}={p} \\ $$$$\begin{cases}{{s}^{\mathrm{2}} +{p}=\mathrm{158}}\\{{p}^{\mathrm{2}} +{s}^{\mathrm{2}} =\mathrm{1028}}\end{cases}\:\:\:\Rightarrow{p}^{\mathrm{2}} −{p}−\mathrm{870}=\mathrm{0}\Rightarrow{p}=\mathrm{30}\:{or}\:−\mathrm{29} \\ $$$$\left.\mathrm{1}\right)\Rightarrow{p}=\mathrm{30}\:\rightarrow{s}^{\mathrm{2}} =\mathrm{128}\rightarrow{s}=\mathrm{8}\sqrt{\mathrm{2}}\Rightarrow{X}^{\mathrm{2}} −\mathrm{8}\sqrt{\mathrm{2}}{X}+\mathrm{30}=\mathrm{0}\rightarrow... \\ $$$${or}\:{s}=−\mathrm{8}\sqrt{\mathrm{2}}\Rightarrow{X}^{\mathrm{2}} +\mathrm{8}\sqrt{\mathrm{2}}{X}+\mathrm{30}=\mathrm{0}\rightarrow.. \\ $$$$ \\ $$$$\left.\mathrm{2}\right)\:{p}=−\mathrm{29}\:\Rightarrow{s}^{\mathrm{2}} =\mathrm{187}\rightarrow{s}=\sqrt{\mathrm{187}}\rightarrow{X}^{\mathrm{2}} −\sqrt{\mathrm{187}}{X}−\mathrm{29}=\mathrm{0} \\ $$$${or}\:\:{s}=−\sqrt{\mathrm{187}}\rightarrow{X}^{\mathrm{2}} +\sqrt{\mathrm{187}}{X}−\mathrm{29}=\mathrm{0}\rightarrow... \\ $$$$ \\ $$

Answered by Frix last updated on 23/Jun/23

Let x=p−q∧y=p+q { ((5p^2 −q^2 −158=0 ⇔ q^2 =5p^2 −158)),((p^4 −2p^2 (q^2 −2)+q^4 −1028=0)) :} p^4 −((315p^2 )/4)+1496=0 p=±((√(187))/2)∨p=±4(√2) ⇒ q=±((√(303))/2)∨q=±(√2) ⇒ x=±(((√(187))+(√(303)))/2)∧y=±(((√(187))−(√(303)))/2) Also exchanging x↔y solves both equations x=±3(√2)∧y=∓5(√2)

$$\mathrm{Let}\:{x}={p}−{q}\wedge{y}={p}+{q} \\ $$$$\begin{cases}{\mathrm{5}{p}^{\mathrm{2}} −{q}^{\mathrm{2}} −\mathrm{158}=\mathrm{0}\:\Leftrightarrow\:{q}^{\mathrm{2}} =\mathrm{5}{p}^{\mathrm{2}} −\mathrm{158}}\\{{p}^{\mathrm{4}} −\mathrm{2}{p}^{\mathrm{2}} \left({q}^{\mathrm{2}} −\mathrm{2}\right)+{q}^{\mathrm{4}} −\mathrm{1028}=\mathrm{0}}\end{cases} \\ $$$${p}^{\mathrm{4}} −\frac{\mathrm{315}{p}^{\mathrm{2}} }{\mathrm{4}}+\mathrm{1496}=\mathrm{0} \\ $$$${p}=\pm\frac{\sqrt{\mathrm{187}}}{\mathrm{2}}\vee{p}=\pm\mathrm{4}\sqrt{\mathrm{2}} \\ $$$$\Rightarrow \\ $$$${q}=\pm\frac{\sqrt{\mathrm{303}}}{\mathrm{2}}\vee{q}=\pm\sqrt{\mathrm{2}} \\ $$$$\Rightarrow \\ $$$${x}=\pm\frac{\sqrt{\mathrm{187}}+\sqrt{\mathrm{303}}}{\mathrm{2}}\wedge{y}=\pm\frac{\sqrt{\mathrm{187}}−\sqrt{\mathrm{303}}}{\mathrm{2}} \\ $$$$\mathrm{Also}\:\mathrm{exchanging}\:{x}\leftrightarrow{y}\:\mathrm{solves}\:\mathrm{both}\:\mathrm{equations} \\ $$$${x}=\pm\mathrm{3}\sqrt{\mathrm{2}}\wedge{y}=\mp\mathrm{5}\sqrt{\mathrm{2}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com