
Question Number 193768 by cortano12 last updated on 19/Jun/23
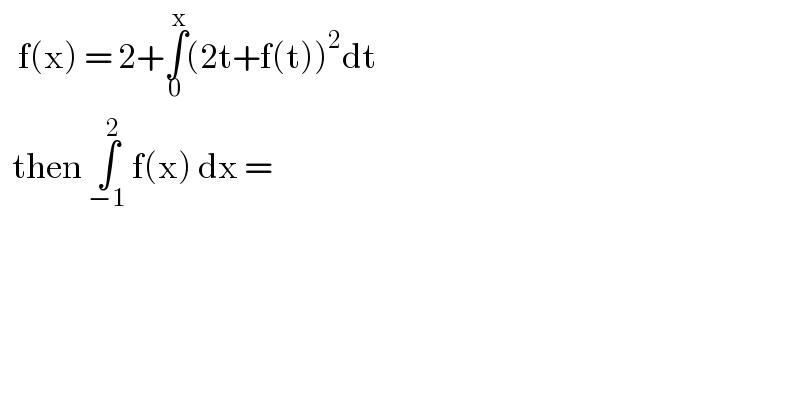
$$\:\:\:\mathrm{f}\left(\mathrm{x}\right)\:=\:\mathrm{2}+\underset{\mathrm{0}} {\overset{\:\mathrm{x}} {\int}}\left(\mathrm{2t}+\mathrm{f}\left(\mathrm{t}\right)\right)^{\mathrm{2}} \mathrm{dt}\: \\ $$$$\:\:\mathrm{then}\:\underset{−\mathrm{1}} {\overset{\mathrm{2}} {\int}}\:\mathrm{f}\left(\mathrm{x}\right)\:\mathrm{dx}\:= \\ $$
Answered by gatocomcirrose last updated on 20/Jun/23
![f′(x)=(2x+f(x))^2 v(x)=2x+y(x)⇒v′(x)=2+f′(x)=2+v(x)^2 (dv/(2+v^2 ))=dx⇒(1/( (√2)))arctan(((v(x))/( (√2))))=x+c_1 ⇒v(x)=(√2)tan((√2)x+C) ⇒f(x)=(√2)tan((√2)x+C)−2x ∫_(−1) ^2 ((√2)tan((√2)x+C)−2x)dx =(√2)∫_(−1) ^2 tan((√2)x+C)dx−3 =[−ln∣cos((√2)x+C)∣]_(−1) ^2 −3 =ln∣cos(C−(√2))∣−ln∣cos(2(√2)+C)∣−3 =ln∣((cos(C−(√2)))/(cos(C+2(√2))))∣−3, C∈R](Q193789.png)
$$\mathrm{f}'\left(\mathrm{x}\right)=\left(\mathrm{2x}+\mathrm{f}\left(\mathrm{x}\right)\right)^{\mathrm{2}} \\ $$$$\mathrm{v}\left(\mathrm{x}\right)=\mathrm{2x}+\mathrm{y}\left(\mathrm{x}\right)\Rightarrow\mathrm{v}'\left(\mathrm{x}\right)=\mathrm{2}+\mathrm{f}'\left(\mathrm{x}\right)=\mathrm{2}+\mathrm{v}\left(\mathrm{x}\right)^{\mathrm{2}} \\ $$$$\frac{\mathrm{dv}}{\mathrm{2}+\mathrm{v}^{\mathrm{2}} }=\mathrm{dx}\Rightarrow\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{arctan}\left(\frac{\mathrm{v}\left(\mathrm{x}\right)}{\:\sqrt{\mathrm{2}}}\right)=\mathrm{x}+\mathrm{c}_{\mathrm{1}} \\ $$$$\Rightarrow\mathrm{v}\left(\mathrm{x}\right)=\sqrt{\mathrm{2}}\mathrm{tan}\left(\sqrt{\mathrm{2}}\mathrm{x}+\mathrm{C}\right) \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\sqrt{\mathrm{2}}\mathrm{tan}\left(\sqrt{\mathrm{2}}\mathrm{x}+\mathrm{C}\right)−\mathrm{2x} \\ $$$$ \\ $$$$\int_{−\mathrm{1}} ^{\mathrm{2}} \left(\sqrt{\mathrm{2}}\mathrm{tan}\left(\sqrt{\mathrm{2}}\mathrm{x}+\mathrm{C}\right)−\mathrm{2x}\right)\mathrm{dx} \\ $$$$=\sqrt{\mathrm{2}}\int_{−\mathrm{1}} ^{\mathrm{2}} \mathrm{tan}\left(\sqrt{\mathrm{2}}\mathrm{x}+\mathrm{C}\right)\mathrm{dx}−\mathrm{3} \\ $$$$=\left[−\mathrm{ln}\mid\mathrm{cos}\left(\sqrt{\mathrm{2}}\mathrm{x}+\mathrm{C}\right)\mid\right]_{−\mathrm{1}} ^{\mathrm{2}} −\mathrm{3} \\ $$$$=\mathrm{ln}\mid\mathrm{cos}\left(\mathrm{C}−\sqrt{\mathrm{2}}\right)\mid−\mathrm{ln}\mid\mathrm{cos}\left(\mathrm{2}\sqrt{\mathrm{2}}+\mathrm{C}\right)\mid−\mathrm{3} \\ $$$$=\mathrm{ln}\mid\frac{\mathrm{cos}\left(\mathrm{C}−\sqrt{\mathrm{2}}\right)}{\mathrm{cos}\left(\mathrm{C}+\mathrm{2}\sqrt{\mathrm{2}}\right)}\mid−\mathrm{3},\:\mathrm{C}\in\mathbb{R} \\ $$
Commented by mr W last updated on 20/Jun/23
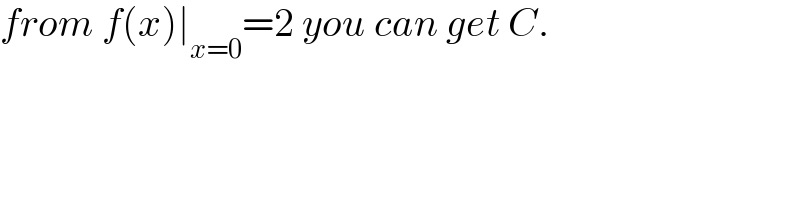
$${from}\:{f}\left({x}\right)\mid_{{x}=\mathrm{0}} =\mathrm{2}\:{you}\:{can}\:{get}\:{C}. \\ $$
